Exercise 10

Question 1

Find the coordinates of the images of the following points under reflection in the x-axis :

(i) (2, -5)

(ii) $\Big(-\dfrac{3}{2}, -\dfrac{1}{2}\Big)$

(iii) (-7, 0).

Answer

(i) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(2, 5) is the image on reflection.

Hence, (2, 5) is the image of the point (2, -5) on reflection in x-axis.

(ii) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'$\Big(-\dfrac{3}{2}, \dfrac{1}{2}\Big)$ is the image on reflection.

Hence, $\Big(-\dfrac{3}{2}, \dfrac{1}{2}\Big)$ is the image of the point $\Big(-\dfrac{3}{2}, -\dfrac{1}{2}\Big)$ on reflection in x-axis.

(iii) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(-7, 0) is the image on reflection.

Hence, (-7, 0) is the image of the point (-7, 0) on reflection in x-axis.

Question 2

Find the coordinates of the images of the following points under reflection in the y-axis :

(i) (2, -5)

(ii) $\Big(-\dfrac{3}{2}, \dfrac{1}{2}\Big)$

(iii) (0, -7).

Answer

(i) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P'(-2, -5) is the image on reflection.

Hence, (-2, -5) is the image of the point (2, -5) on reflection in y-axis.

(ii) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P'$(\dfrac{3}{2}, \dfrac{1}{2})$ is the image on reflection.

Hence, $(\dfrac{3}{2}, \dfrac{1}{2})$ is the image of the point $(-\dfrac{3}{2}, -\dfrac{1}{2})$ on reflection in y-axis.

(iii) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P'(0, -7) is the image on reflection.

Hence, (0, -7) is the image of the point (0, -7) on reflection in y-axis.

Question 3

Find the coordinates of the images of the following points under reflection in the origin :

(i) (2, -5)

(ii) $\Big(-\dfrac{3}{2}, -\dfrac{1}{2}\Big)$

(iii) (0, 0).

Answer

(i) We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(-2, 5) is the image on reflection.

Hence, (-2, 5) is the image of the point (2, -5) on reflection in origin.

(ii) We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'$(\dfrac{3}{2}, \dfrac{1}{2})$ is the image on reflection.

Hence, $(\dfrac{3}{2}, \dfrac{1}{2})$ is the image of the point $(-\dfrac{3}{2}, -\dfrac{1}{2})$ on reflection in origin.

(iii) We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(0, 0) is the image on reflection.

Hence, (0, 0) is the image of the point (0, 0) on reflection in origin.

Question 4

The image of a point P under reflection in the x-axis is (5, -2). Write down the coordinates of P.

Answer

Since, (5, -2) is the image of P under reflection in x-axis, from graph we get,

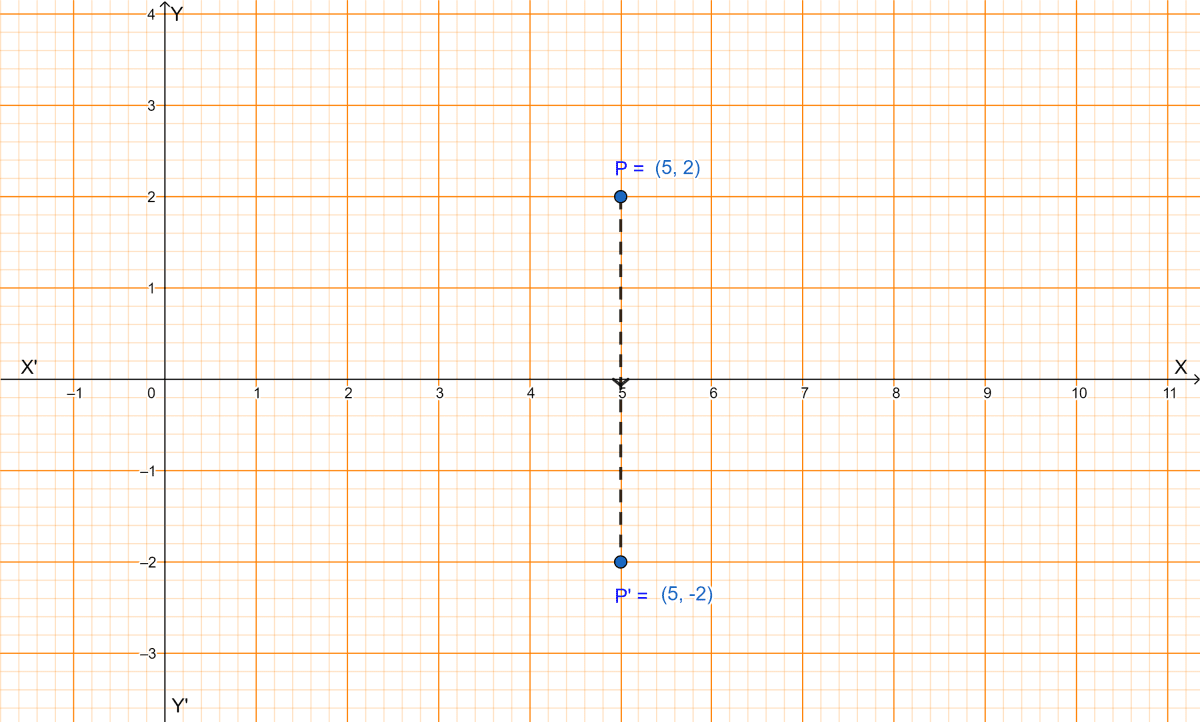
The coordinates of P are (5, 2).

Question 5

A point P is reflected in the x-axis. Coordinates of its image are (8, -6).

(i) Find the coordinates of P.

(ii) Find the coordinates of the image of P under reflection in the y-axis.

Answer

(i) Since, (8, -6) is the image of P under reflection in x-axis, let this point be P' so from graph we get,

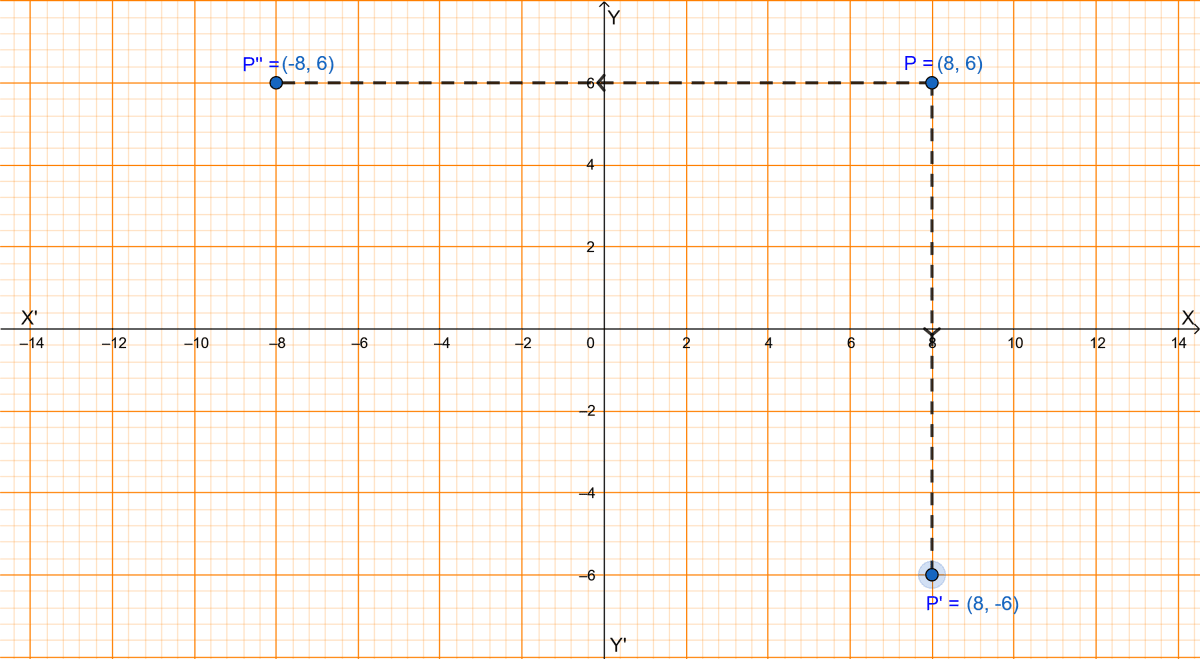
The coordinates of P are (8, 6).

(ii) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P''(-8, 6) is the image on reflection.

Hence, (-8, 6) is the image of the point (8, 6) on reflection in y-axis.

Question 6

A point P is reflected in the origin. Coordinates of its image are (2, -5). Find

(i) the coordinates of P.

(ii) the coordinates of the image of P in the x-axis.

Answer

(i) Since, (2, -5) is the image of P under reflection in origin, let this point be P' so from graph we get,

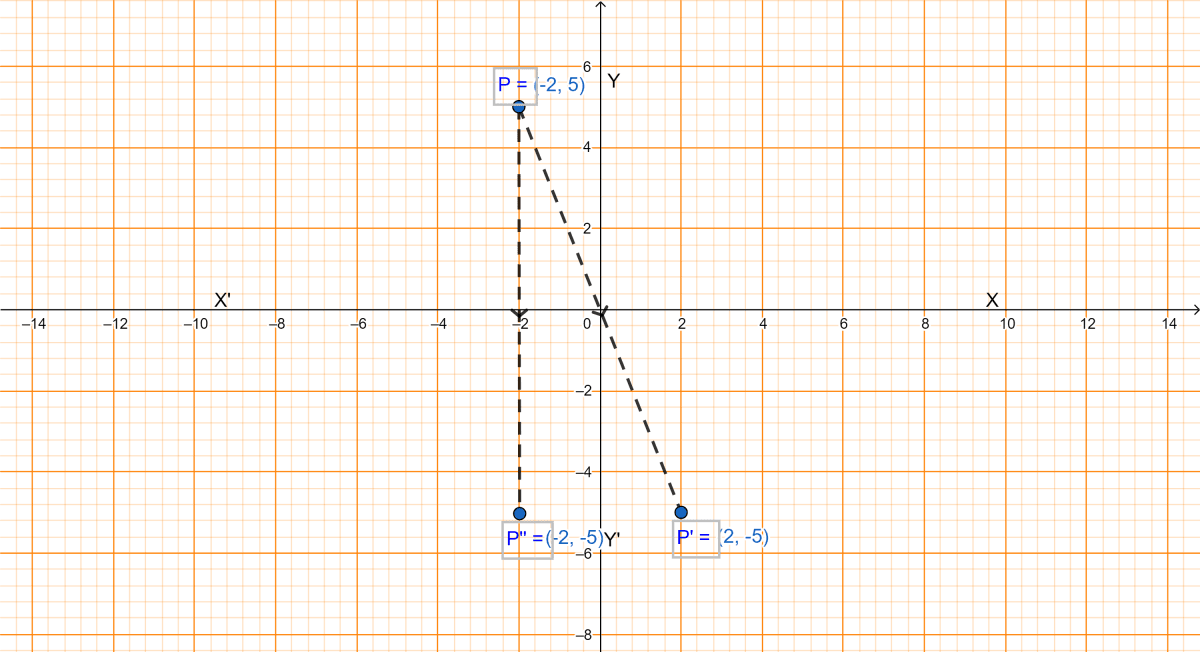
The coordinates of P are (-2, 5).

(ii) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P''(-2, -5) is the image on reflection.

Hence, P''(-2, -5) is the image of the point P(-2, 5) on reflection in x-axis.

Question 7(i)

The point P(2, 3) is reflected in the line x = 4 to the point P'. Find the coordinates of the point P'.

Answer

We know that the reflection of the point (x, y) in the line x = a is the point (-x + 2a, y).

∴ The image of the point P(2, 3) under reflection in the line x = 4 is the point P'(-2 + 2 × 4, 3) i.e., the point P'(6, 3).

The coordinates of the point P' is (6, 3).

Question 7(ii)

Find the image of the point P(1, -2) in the line x = -1.

Answer

We know that the reflection of the point (x, y) in the line x = a is the point (-x + 2a, y).

∴ The image of the point P(1, -2) under reflection in the line x = -1 is the point P'(-1 + 2 × (-1), -2) i.e., the point P'(-3, -2).

The coordinates of the point P' is (-3, -2).

Question 8(i)

The point P(2, 4) on reflection in the line y = 1 is mapped onto P'. Find the coordinates of P'.

Answer

We know that the reflection of the point (x, y) in the line y = a is the point (x, -y + 2a).

∴ The image of the point P(2, 4) under reflection in the line y = 1 is the point P'(2, -4 + 2 × 1) i.e., the point P'(2, -2).

The coordinates of the point P' is (2, -2).

Question 8(ii)

Find the image of the point P(-3, -5) in the line y = -2.

Answer

We know that the reflection of the point (x, y) in the line y = a is the point (x, -y + 2a).

∴ The image of the point P(-3, -5) under reflection in the line y = -2 is the point P'(-3, -(-5) + 2 × (-2)) i.e., the point P'(-3, 1).

Hence, the image of the point (-3, -5) in y = -2 is (-3, 1).

Question 9

The point P(-4, -5) on reflection in y-axis is mapped on P'. The point P' on reflection in the origin is mapped on P''. Find the coordinates of P' and P''. Write down a single transformation that maps P onto P''.

Answer

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P(-4, -5) becomes P'(4, -5) on reflection in y-axis.

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(4, -5) becomes P''(-4, 5) on reflection in origin.

On reflecting the point P(-4, -5) in x-axis, it becomes (-4, 5) which are the coordinates of P''.

Hence, the single transformation that maps P(-4, -5) onto P''(-4, 5) is reflection of point P in x-axis.

Question 10

Write down the coordinates of the image of the point (3, -2) when:

(i) reflected in the x-axis.

(ii) reflected in the y-axis.

(iii) reflected in the x-axis followed by reflection in the y-axis.

(iv) reflected in the origin.

Answer

(i) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(3, 2) is the image on reflection.

Hence, (3, 2) is the image of the point (3, -2) on reflection in x-axis.

(ii) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Point P'(-3, -2) is the image on reflection.

Hence, (-3, -2) is the image of the point (3, -2) on reflection in y-axis.

(iii) On reflection in x-axis the point P(3, -2) becomes P'(3, 2) which on further reflection in y-axis becomes P''(-3, 2) as shown in the graph.

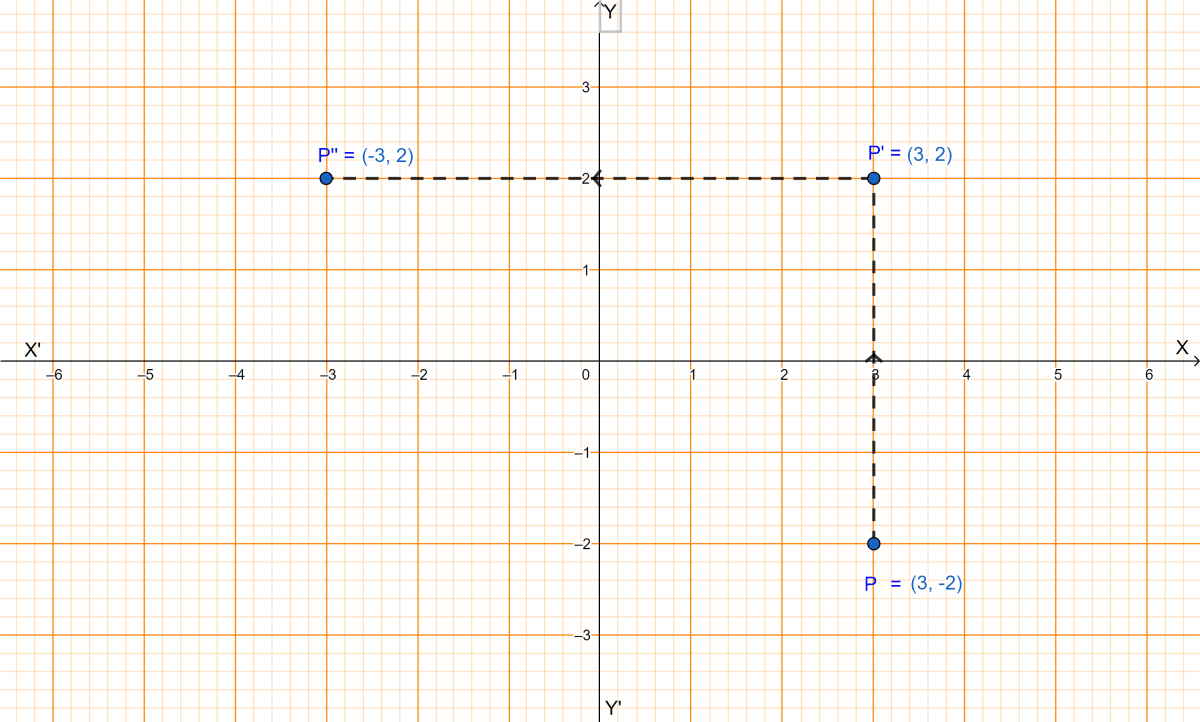
Hence, P''(-3, 2) is the final image after reflections.

(iv) We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(-3, 2) is the image on reflection.

Hence, (-3, 2) is the image of the point (3, -2) on reflection in origin.

Question 11

Find the coordinates of the image of (3, 1) under reflection in x-axis followed by reflection in the line x = 1.

Answer

We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point P'(3, -1) is the image on reflection of (3, 1) in x-axis.

We know that the reflection of the point (x, y) in the line x = a is the point (-x + 2a, y).

∴ The image of the point P'(3, -1) under reflection in the line x = 1 is the point P'(-3 + 2 × 1, -1) i.e., the point P'(-1, -1).

Hence, the coordinates of the final image is P''(-1, -1).

Question 12

If P'(-4, -3) is the image of a point P under reflection in the origin, find

(i) the coordinates of P.

(ii) the coordinates of the image of P under reflection in the line y = -2.

Answer

(i) Since, P'(-4, -3) is the image of P under reflection in the origin, from graph P(4, 3).

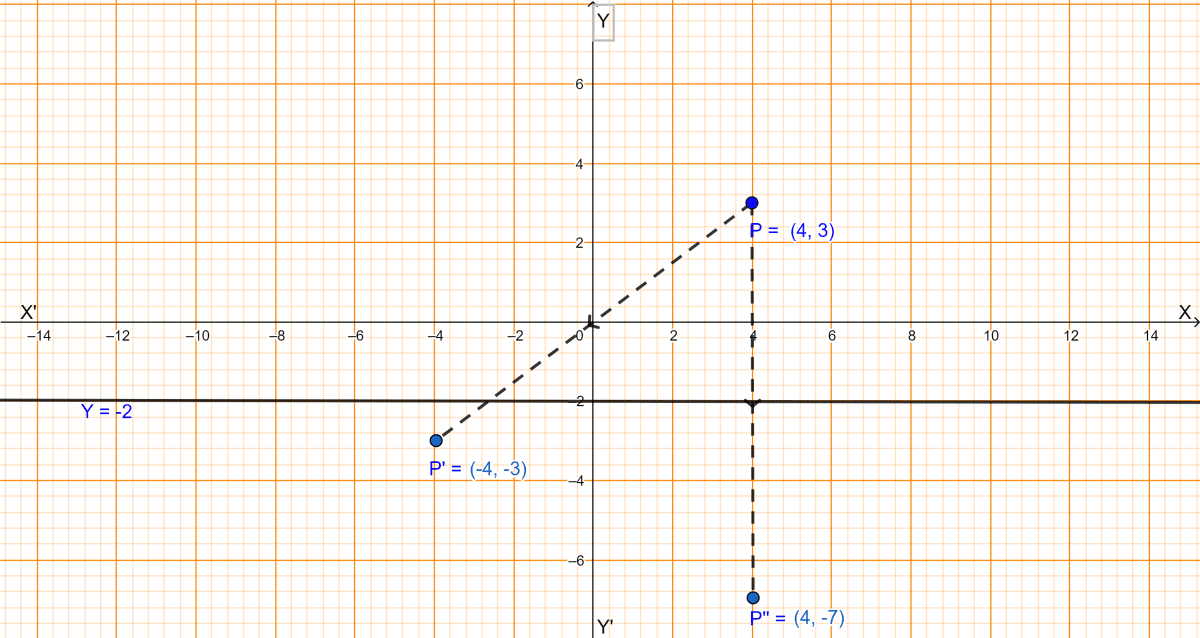
Hence, the coordinates of P are (4, 3).

(ii) We know that the reflection of the point (x, y) in the line y = a is the point (x, -y + 2a).

∴ The image of the point P(4, 3) under reflection in the line y = -2 is the point P''(4, -(3) + 2 × (-2)) i.e., the point P''(4, -7).

Hence, the coordinates of P under reflection in the line y = -2 is (4, -7).

Question 13

A point P(a, b) is reflected in the x-axis to P'(2, -3), write down the values of a and b. P'' is the image of P, when reflected in the y-axis. Write down the coordinates of P''. Find the coordinates of P''', when P is reflected in the line, parallel to y-axis such that x = 4.

Answer

Since, P'(2, -3) is the image of P under reflection in the x-axis, from graph we get P(2, 3).

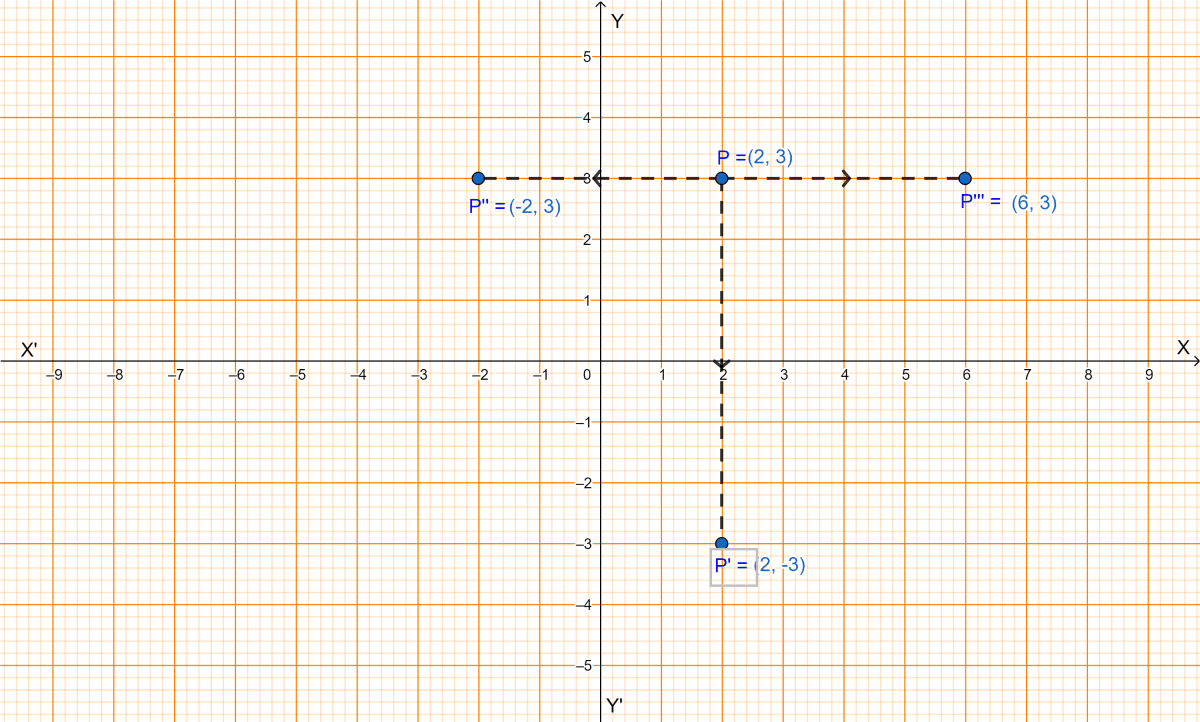
∴ The coordinates of P are (2,3), comparing with P(a, b) we get, a = 2 and b = 3.

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

Since, P'' is image on reflection of P in y-axis.

∴ The coordinates of P'' are (-2,3).

We know that the reflection of the point (x, y) in the line x = a is the point (-x + 2a, y).

∴ The image of the point P(2, 3) under reflection in the line x = 4 is the point P'''(-2 + 2 × 4, 3) i.e the point P'''(6, 3).

Hence, the value of a = 2, b = 3 and the coordinates of P''(-2, 3), P'''(6, 3).

Question 14

(i) Point P(a, b) is reflected in the x-axis to P'(5, -2). Write down the values of a and b.

(ii) P'' is the image of P when reflected in the y-axis. Write down the coordinates of P''.

(iii) Name a single transformation that maps P' into P''.

Answer

(i) Since, P'(5, -2) is the image of P under reflection in the x-axis, from graph P(5, 2).

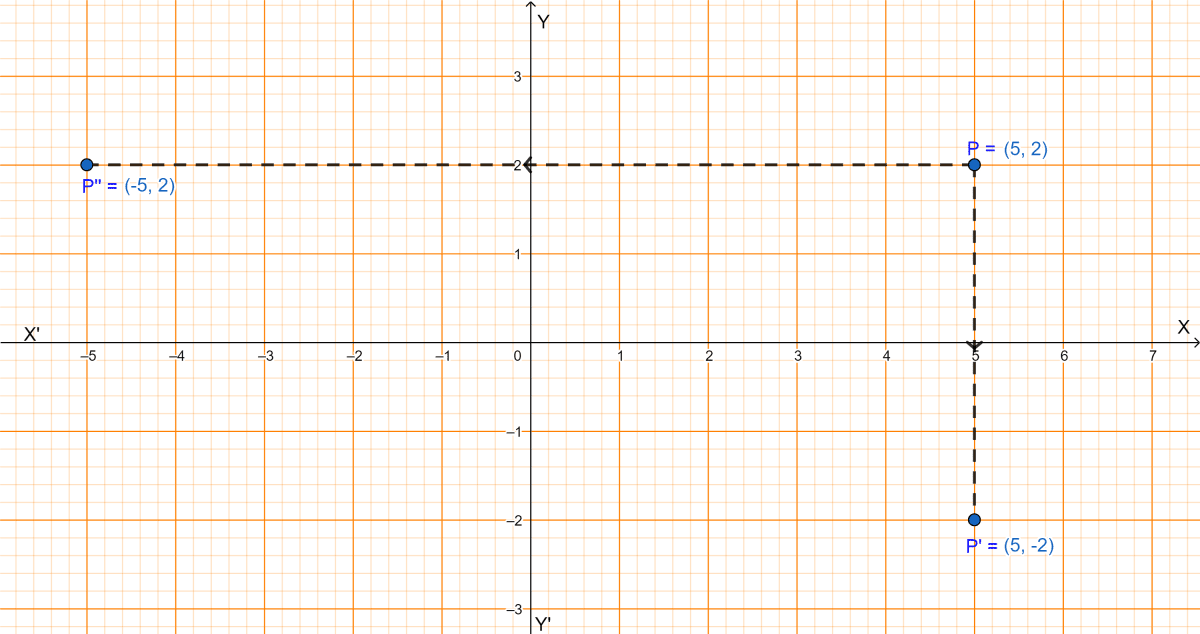
∴ The coordinates of P are (5,2), comparing with P(a, b) we get, a = 5 and b = 2.

Hence, the value of a = 5 and b = 2.

(ii) We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

Since, P'' is image on reflection of P(5, 2) in y-axis.

Hence, the coordinates of P'' are (-5, 2).

(iii) The single transformation that maps P'(5, -2) into P''(-5, 2) is reflection in the origin.

Question 15

Points A and B have coordinates (2, 5) and (0, 3). Find :

(i) the image A' of A under reflection in the x-axis.

(ii) the image B' of B under reflection in the line AA'.

Answer

The graph with the points A (2, 5), B (0, 3) and their images A' and B' is shown below:

(i) We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point A'(2, -5) is the image on reflection of A(2, 5) in x-axis.

The coordinates of A' are (2, -5).

(ii) From graph we get,

The coordinates of B' are (4, 3).

Question 16

Plot the points A(2, -3), B(-1, 2) and C(0, -2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent ?

Answer

The points A(2, -3), B(-1, 2) and C(0, -2) are plotted on the graph below:

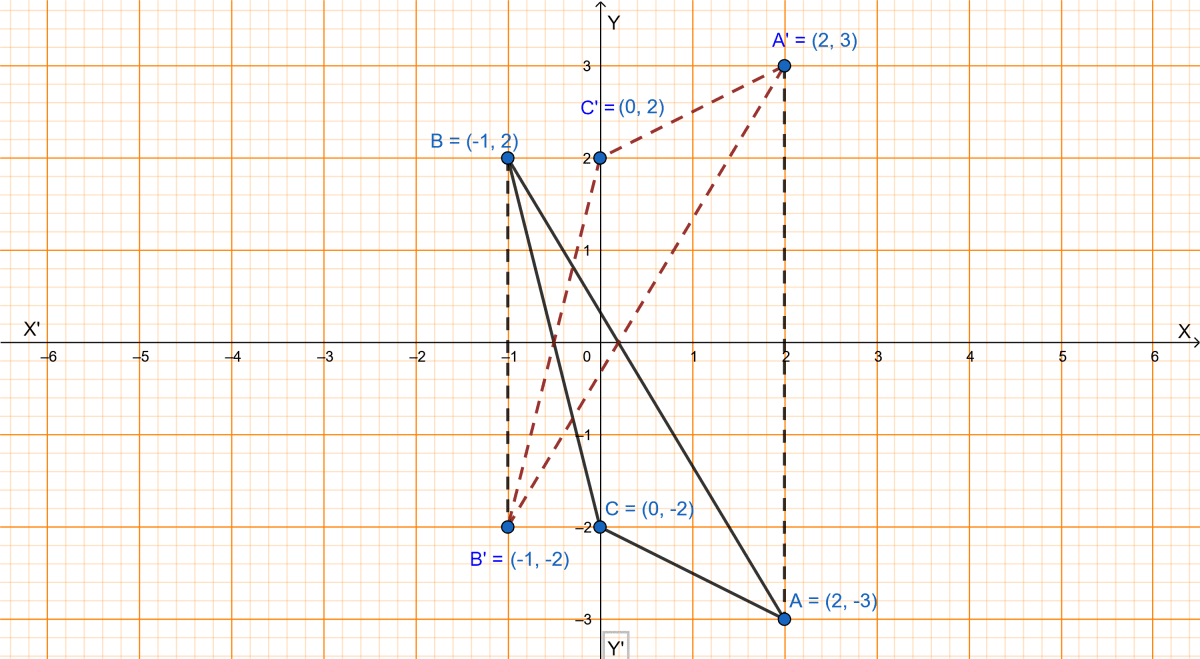
From graph we get,

AB = A'B'
AC = A'C'
BC = B'C'

Hence, △ABC and △A'B'C' are congruent.

Question 17

The points (6, 2), (3, -1) and (-2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.

Answer

The right angled triangle with points (6, 2), (3, -1) and (-2, 4) as vertices is plotted below:

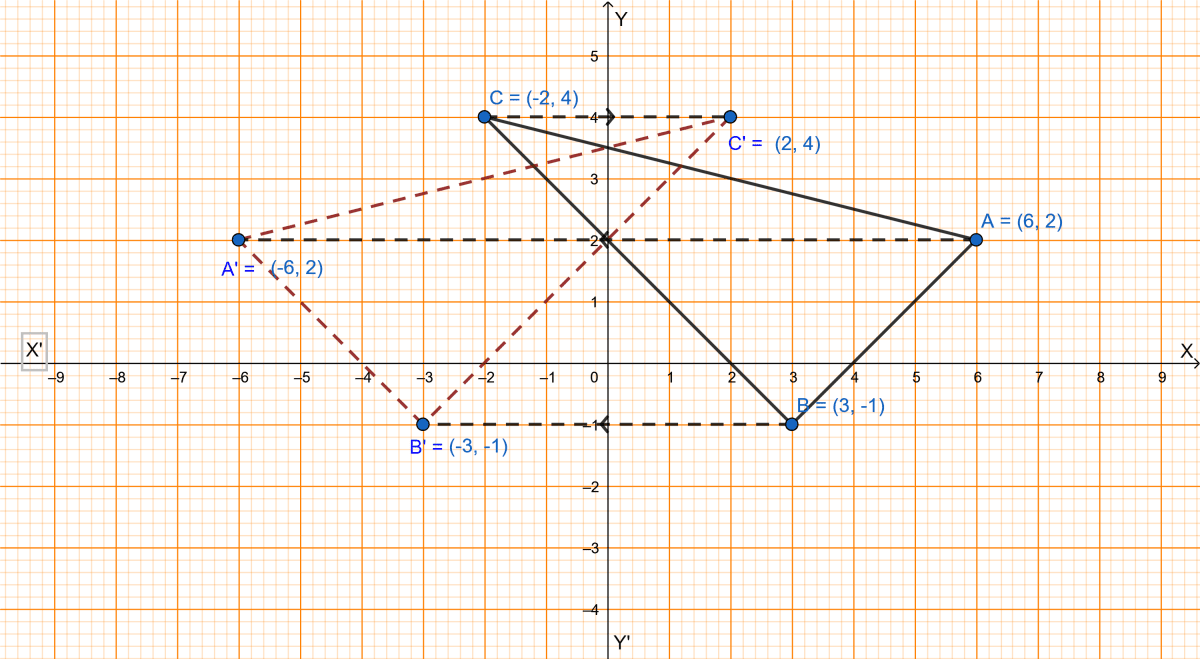
From graph we get,

AB = A'B'
AC = A'C'
BC = B'C'

∴ △ABC and △A'B'C' are congruent.

Since, △ABC is a right angled triangle hence, △A'B'C' is also a right angled triangle.

Question 18

The triangle ABC where A(1, 2), B(4, 8), C(6, 8) is reflected in the x-axis to triangle A'B'C'. The triangle A'B'C' is then reflected in the origin to the triangle A''B''C''. Write down the coordinates of A'', B'', C''. Write down a single transformation that maps ABC onto A''B''C''.

Answer

We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of
⇒ A(1, 2) on reflection in x-axis becomes A'(1, -2).
⇒ B(4, 8) on reflection in x-axis becomes B'(4, -8).
⇒ C(6, 8) on reflection in x-axis becomes C'(6, -8).

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of
⇒ A'(1, -2) on reflection in origin becomes A''(-1, 2).
⇒ B'(4, -8) on reflection in origin becomes B''(-4, 8).
⇒ C'(6, -8) on reflection in origin becomes C''(-6, 8).

A single transformation that maps A ⇒ A'', B ⇒ B'' and C ⇒ C'' is reflection in y-axis.

Hence, the coordinates of A'', B'' and C'' are (-1, 2), (-4, 8) and (-6, 8) respectively, and a single transformation that maps ABC to A''B''C'' is reflection in y-axis.

Question 19

The image of a point P on reflection in a line l is a point P'. Describe the location of the line l.

Answer

Given, P on reflection in a line l is a point P'.

Hence, The line l is the right bisector of the line segment PP'.

Question 20

Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate (i) the x-axis (ii) the y-axis and (iii) the origin.

Answer

Given, Q is the image of P on reflection in y-axis and midpoint of PQ is invariant on reflection in x-axis.

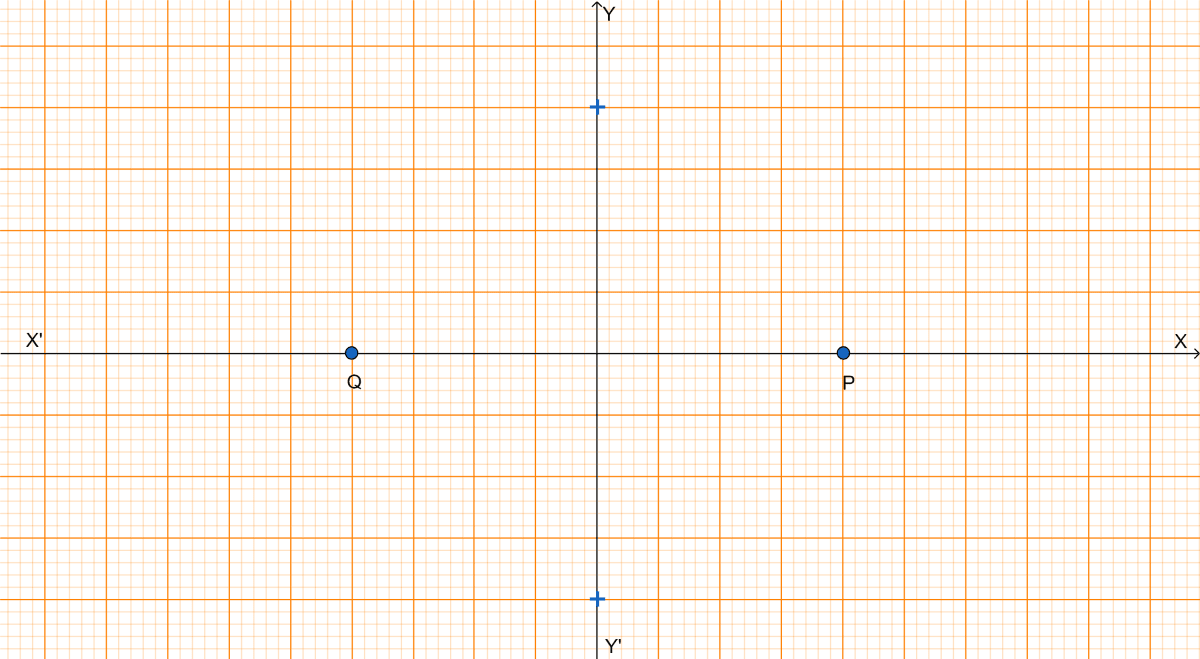
From graph we get,

(i) x-axis will be the line joining the points P and Q.

(ii) The line perpendicular bisector of the line segment PQ is the y-axis.

(iii) The origin will be the mid point of the line segment PQ.

Question 21

The point (-3, 0) on reflection in a line is mapped as (3, 0) and the point (2, -3) on reflection in the same line is mapped as (-2, -3).

(i) Name the mirror line.

(ii) Write the coordinates of the image of (-3, -4) in the mirror line.

Answer

Given, the point (-3, 0) is the image of point (3, 0) and (-2, -3) is the image of point (2, -3) in the same line.

Considering graph,

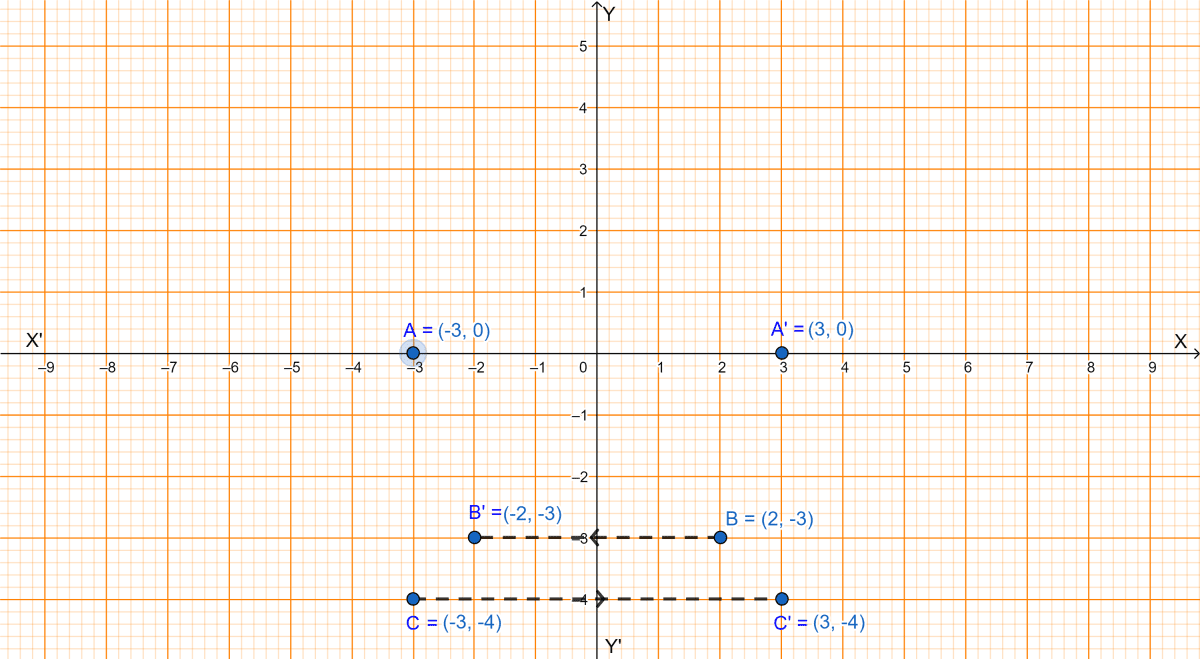
(i) The mirror line is y-axis.

(ii) Since, the mirror line is y-axis. We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

Let C be the point (-3, -4).

∴ C' (3, -4) is the image on reflection of C (-3, -4) in y-axis.

Hence, the reflection of (-3, -4) in y-axis is (3, -4).

Question 22

Use graph paper for this question (take 2cm = 1 unit along both x and y axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, -2), C(0, -1) and D(0, 1).

(i) Reflect quadrilateral ABCD on the y-axis and name it as A'B'CD.

(ii) Write down the coordinates of A' and B'.

(iii) Name two points which are invariant under the above reflection.

(iv) Name the polygon A'B'CD.

Answer

(i) Reflected quadrilateral A'B'CD is shown in the graph below:

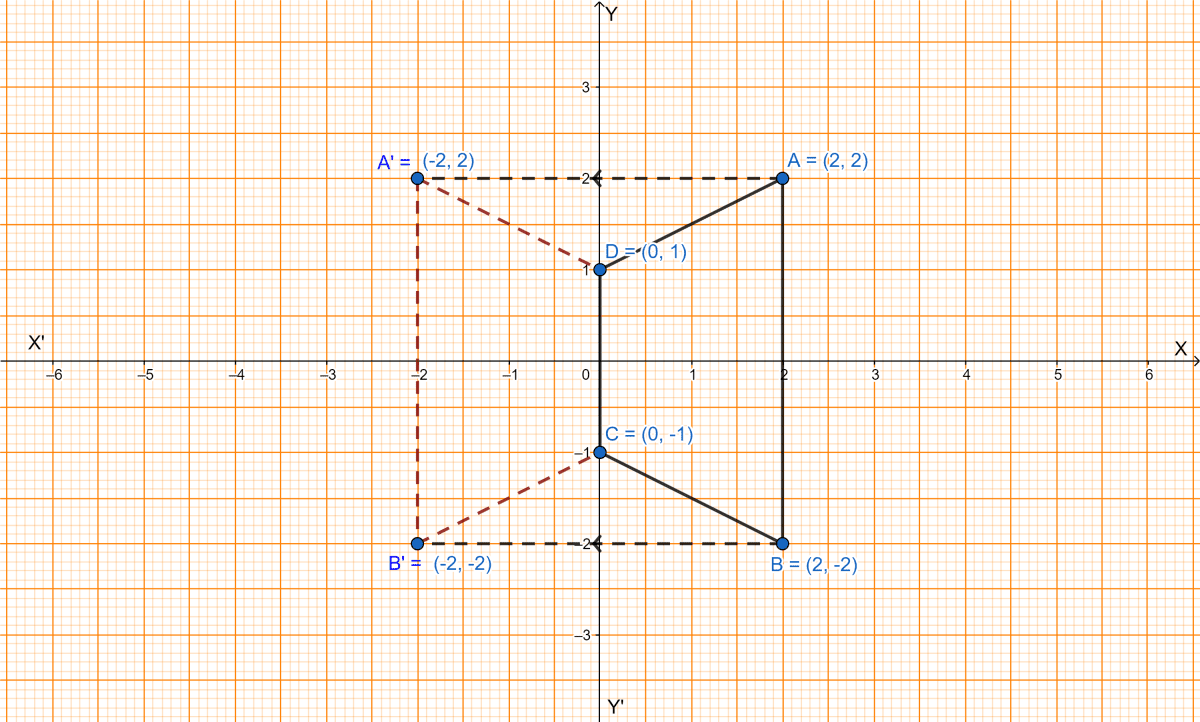
(ii) From graph we get,

The coordinates of A' and B' are (-2, 2) and (-2, -2) respectively.

(iii) From graph we get,

The two points which are invariant under the above reflection are C and D.

(iv) From graph we get,

The polygon(A'B'CD) formed is an isosceles trapezium.

Question 23

Use a graph sheet for this question. Take 1cm = 1 unit along both x and y-axes.

(i) Plot the points : A(0, 5), B(3, 0), C(1, 0) and D(1, -5).

(ii) Reflect the points B, C and D on the y-axis and name them as B', C' and D' respectively.

(iii) Write down the coordinates of B', C' and D'.

(iv) Join the points A, B, C, D, D', C', B', A in order and give a name to the closed figure ABCDD'C'B'.

Answer

Parts (i) and (ii) are solved in the graph below:

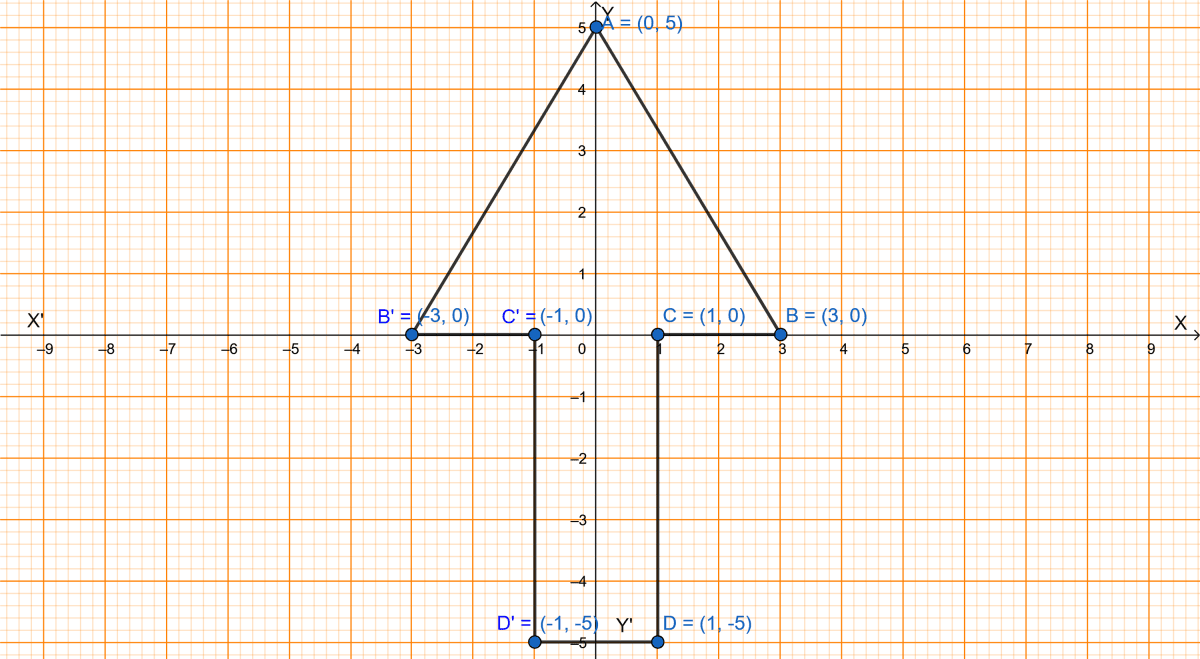
(iii) From graph we get,

The coordinates of B', C' and D' are (-3, 0), (-1, 0) and (-1, -5) respectively.

(iv) From graph we get,

The closed figure (ABCDD'C'B') formed is a heptagon/septagon (i.e., a polygon with seven sides).

Question 24

Use graph paper for this question.

(i) The point P(2, -4) is reflected about the line x = 0 to get the image Q. Find the coordinates of Q.

(ii) Point Q is reflected about the line y = 0 to get the image R. Find the coordinates of R.

(iii) Name the figure PQR.

(iv) Find the area of the figure PQR.

Answer

The graph is given below:

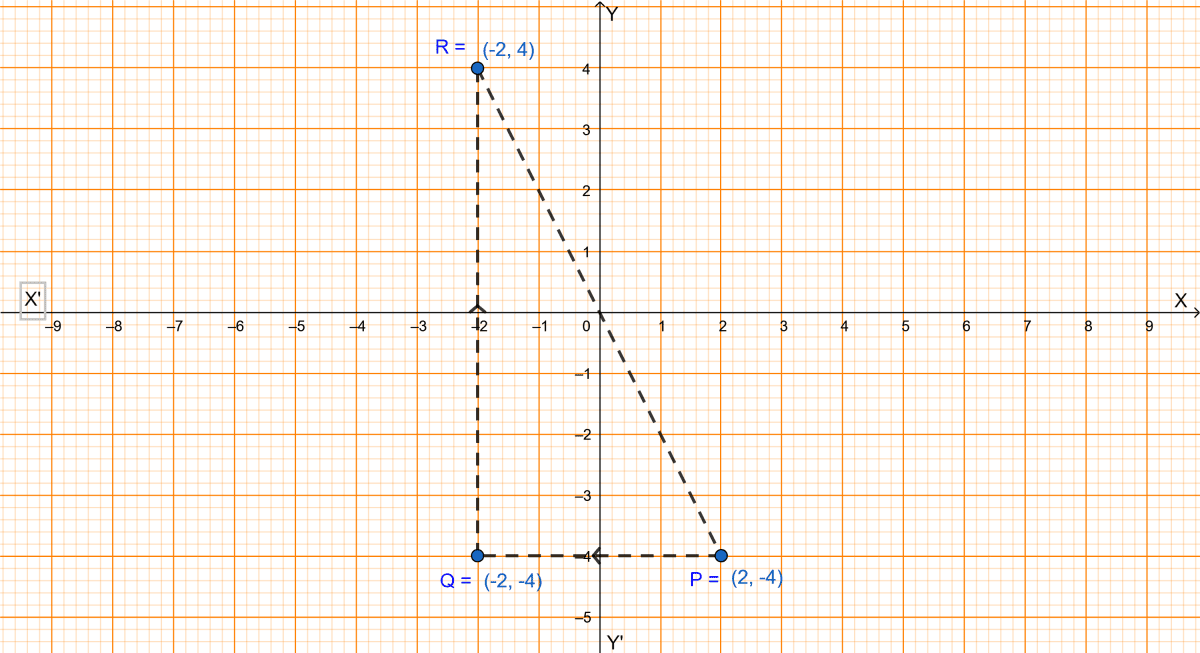
(i) From graph we get,

The coordinate of Q is (-2, -4).

(ii) From graph we get,

The coordinate of R is (-2, 4).

(iii) From graph we get,

The image formed is right angled triangle.

(iv) We know that in the graph,

One block represents 1 unit.

Area of right angle triangle = $\dfrac{1}{2} \times$ base × height.

$= \dfrac{1}{2} \times \text{PQ} \times \text{QR} \\[1em] = \dfrac{1}{2} \times 4 \text{ units } \times 8 \text{ units } \\[1em] = 16 \text{ sq. units}.$

Hence, the area of figure PQR is 16 sq. units.

Question 25

Using a graph paper, plot the points A(6, 4) and B(0, 4).

(i) Reflect A and B in the origin to get images A' and B'.

(ii) Write the coordinates of A' and B'.

(iii) State the geometrical name for the figure ABA'B'.

(iv) Find its perimeter.

Answer

(i) A' and B' are plotted on the graph below:

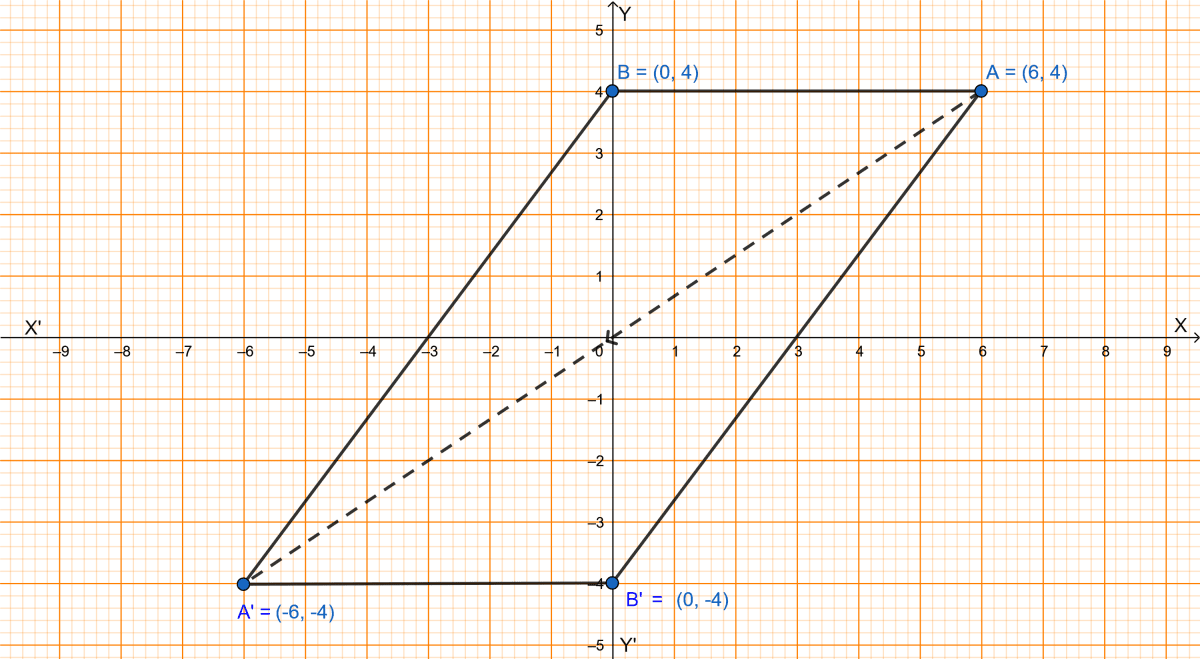
(ii) From graph we get,

The coordinates of A' and B' are (-6, -4) and (0, -4) respectively.

(iii) From graph we get,

ABA'B' formed is a parallelogram.

(iv) From graph we get,

By pythagoras theorem,

$\text{AB}' = \sqrt{(\text{AB})^2 + (\text{BB}')^2} \\[1em] = \sqrt{6^2 + 8^2} \\[1em] = \sqrt{100} \\[1em] = 10 \text{ units }.$

Perimeter = Sum of all sides = AB' + B'A' + A'B + BA = 10 + 6 + 6 + 10 = 32 units.

Hence, the perimeter of the parallelogram is 32 units.

Question 26

Use graph paper to solve this question.

(i) Plot the points A(4, 6) and B(1, 2).

(ii) If A' is the image of A when reflected in the x-axis, write the coordinates of A'.

(iii) If B' is the image of B when reflected in the line AA', write the coordinates of B'.

(iv) Give the geometrical name for the figure ABA'B'.

Answer

(i) Points A(4, 6) and B(1, 2) are plotted on the graph below:

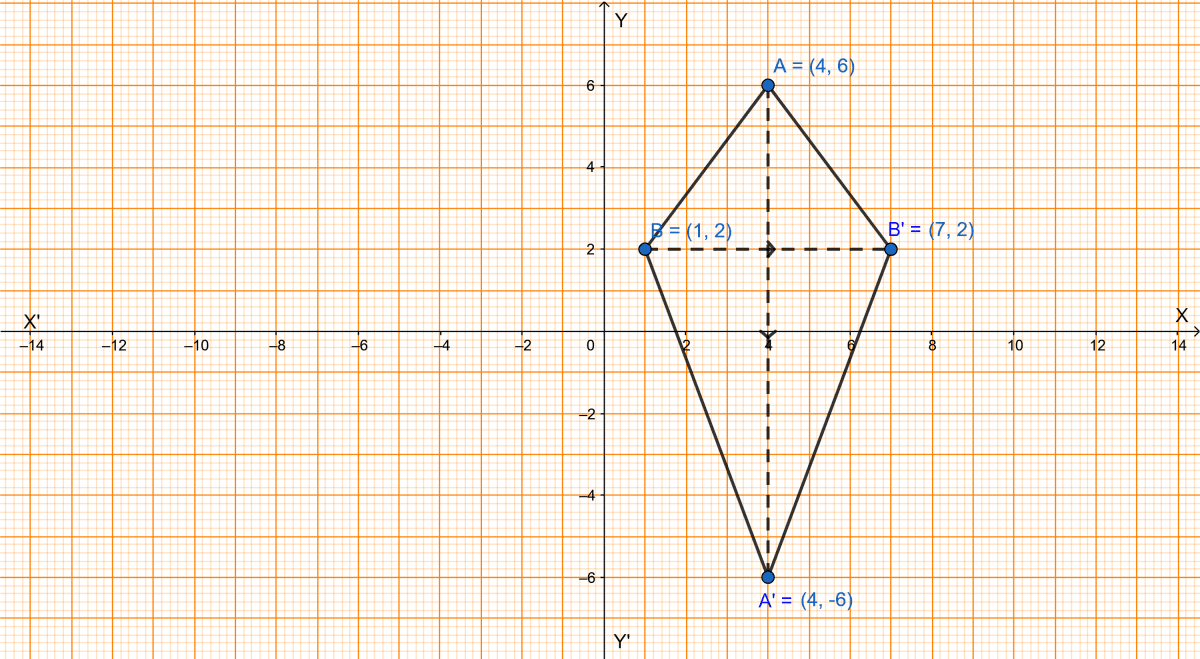
(ii) From graph we get,

The coordinates of point A' = (4, -6).

(iii) From graph we get,

The coordinates of point B' = (7, 2).

(iii) From graph we get,

ABA'B' formed is a kite (or a Quadrilateral).

Question 27

The points A(2, 3), B(4, 5) and C(7, 2) are the vertices of △ABC.

(i) Write down the coordinates of A₁, B₁, C₁ if △A₁B₁C₁ is the image of △ABC when reflected in the origin.

(ii) Write down the coordinates of A₂, B₂, C₂ if △A₂B₂C₂ is the image of △ABC when reflected in the x-axis.

(iii) Assign the special name to quadrilateral BCC₂B₂ and find its area.

Answer

The graph is shown below:

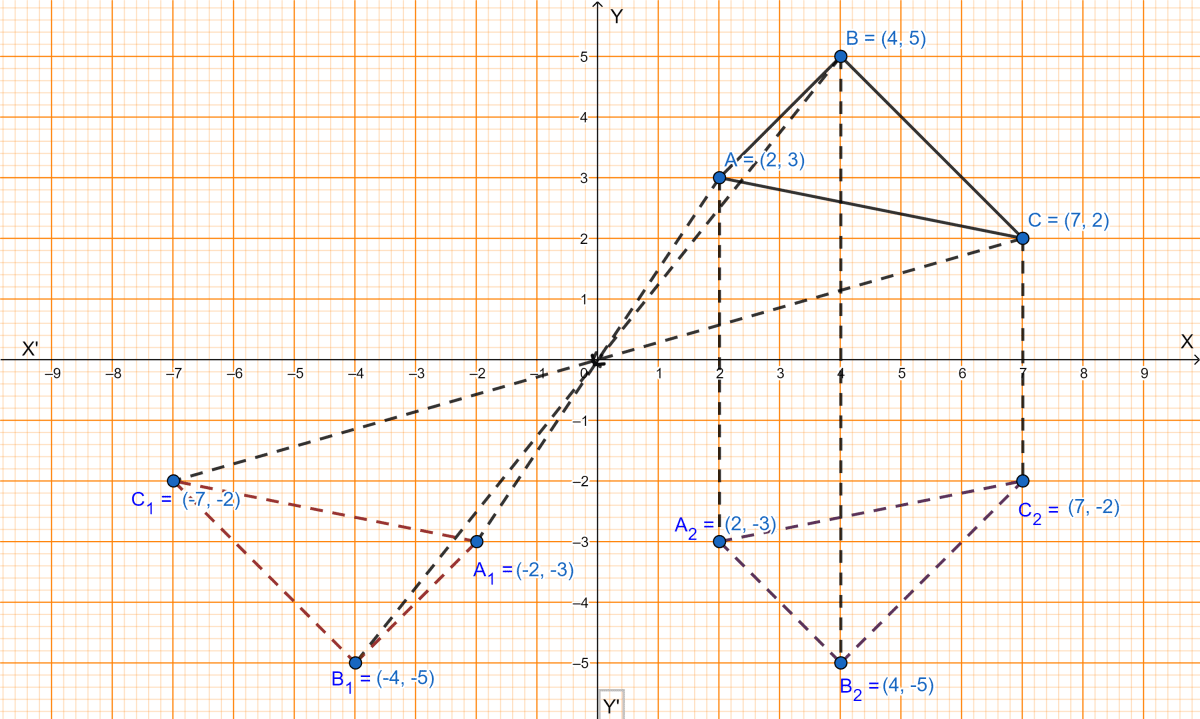
(i) From graph we get,

The coordinates of A₁, B₁, C₁ are (-2, -3), (-4, -5) and (-7, -2) respectively.

(ii) From graph we get,

The coordinates of A₂, B₂, C₂ are (2, -3), (4, -5) and (7, -2) respectively.

(iii) From graph we get,

BCC₂B₂ formed is an isosceles trapezium.

We know that,

Area of trapezium = $\dfrac{1}{2} \times$ sum of parallel sides $\times$ distance between them

$= \dfrac{1}{2} \times (\text{BB}_2 + \text{CC}_2) \times 3 \\[1em] = \dfrac{1}{2} \times (10 + 4) \times 3 \\[1em] = \dfrac{1}{2} \times 42 \\[1em] = 21 \text{ sq. units}$

Question 28

The point P(3, 4) is reflected to P' in the x-axis and O' is the image of O(origin) in the line PP'. Find :

(i) the coordinates of P' and O'.

(ii) the length of segments PP' and OO'.

(iii) the perimeter of the quadrilateral POP'O'.

Answer

The graph is shown below:

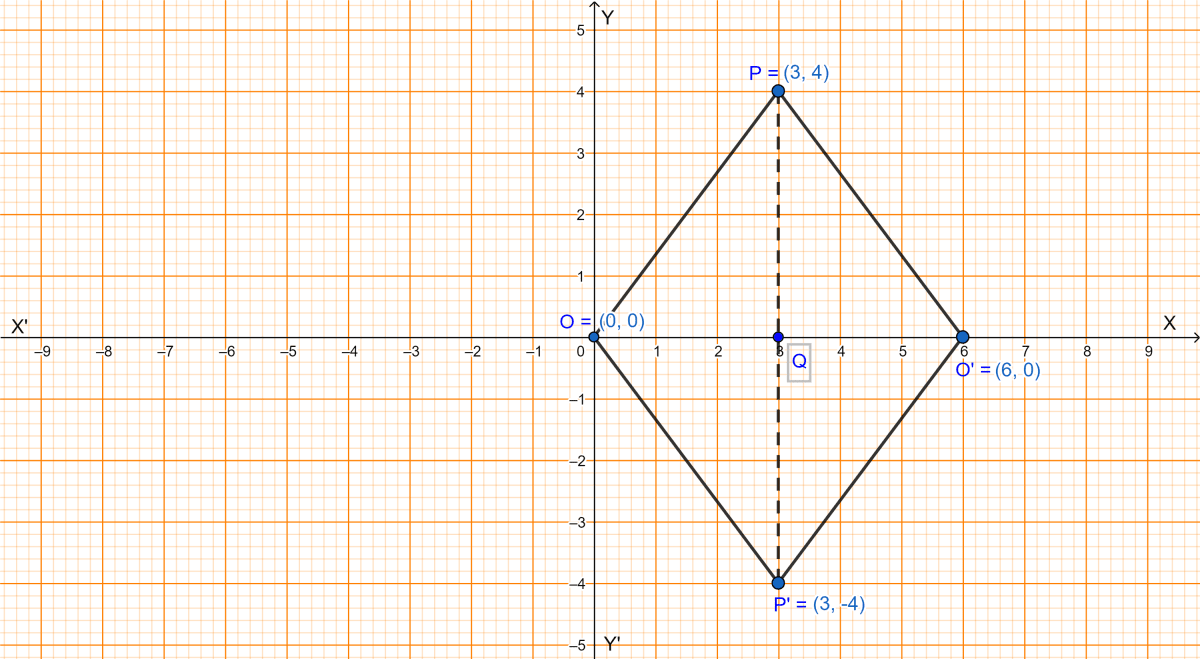
(i) From graph we get,

The coordinates of P' and O' are (3, -4) and (6, 0) respectively.

(ii) From graph we get,

Length of PP' = 8 units and OO' = 6 units.

(iii) OP = PO' = O'P' = P'O, as all are hypotenuse for same base and perpendicular.

∴ Perimeter of POP'O' is = 4 × OP

$= 4 \times \sqrt{(OQ)^2 + (PQ)^2} \\[1em] = 4 \times \sqrt{(3)^2 + (4)^2} \\[1em] = 4 \times \sqrt{9 + 16} \\[1em] = 4 \times \sqrt{25} \\[1em] = 4 \times 5 \\[1em] = 20 \text{ units }.$

The perimeter of the quadrilateral POP'O' is 20 units.

Question 29

Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have coordinates (0, 5) and (-2, 4).

(i) P is invariant when reflected in an axis. Name the axis.

(ii) Find the image of Q on reflection in the axis found in (i).

(iii) (0, k) on reflection in the origin is invariant. Write the value of k.

(iv) Write the coordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis.

Answer

The graph for the question is shown below:

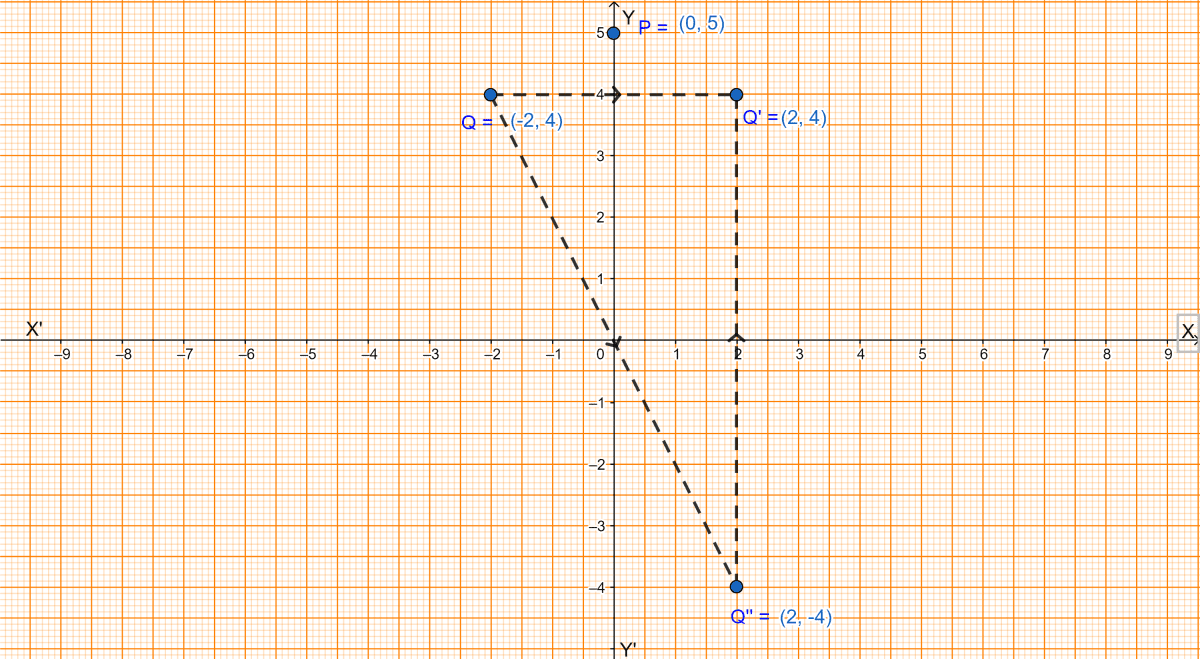
(i) The point P(0, 5) is invariant in y-axis.

(ii) From graph we get,

The image of Q(-2, 4) on reflection in y-axis is Q'(2, 4).

(iii) Given, (0, k) on reflection in the origin is invariant.

From graph we get, (0, 0) on reflection in the origin is invariant. Comparing (0, k) with (0, 0) we get k = 0.

Hence, the value of k = 0.

(iv) From graph we get,

The coordinates of image of Q after reflection in origin and then in x-axis is (2, 4).

Multiple Choice Questions

Question 1

The reflection of the point P(-2, 3) in the x-axis is

1. (2, 3)

2. (2, -3)

3. (-2, -3)

4. (-2, 0)

Answer

We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of point P(-2, 3) on reflection in x-axis is (-2, -3).

Hence, Option 3 is the correct option.

Question 2

The reflection of the point P(-2, 3) in the y-axis is

1. (2, 3)

2. (2, -3)

3. (-2, -3)

4. (0, 3)

Answer

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Coordinates of point P(-2, 3) on reflection in y-axis is (2, 3).

Hence, Option 1 is the correct option.

Question 3

If the image of the point P under reflection in the x-axis is (-3, 2), then the coordinates of the point P are

1. (3, 2)

2. (-3, -2)

3. (3, -2)

4. (-3, 0)

Answer

Since, (-3, 2) is the image of the point P on reflection in x-axis so from graph P(-3, -2).

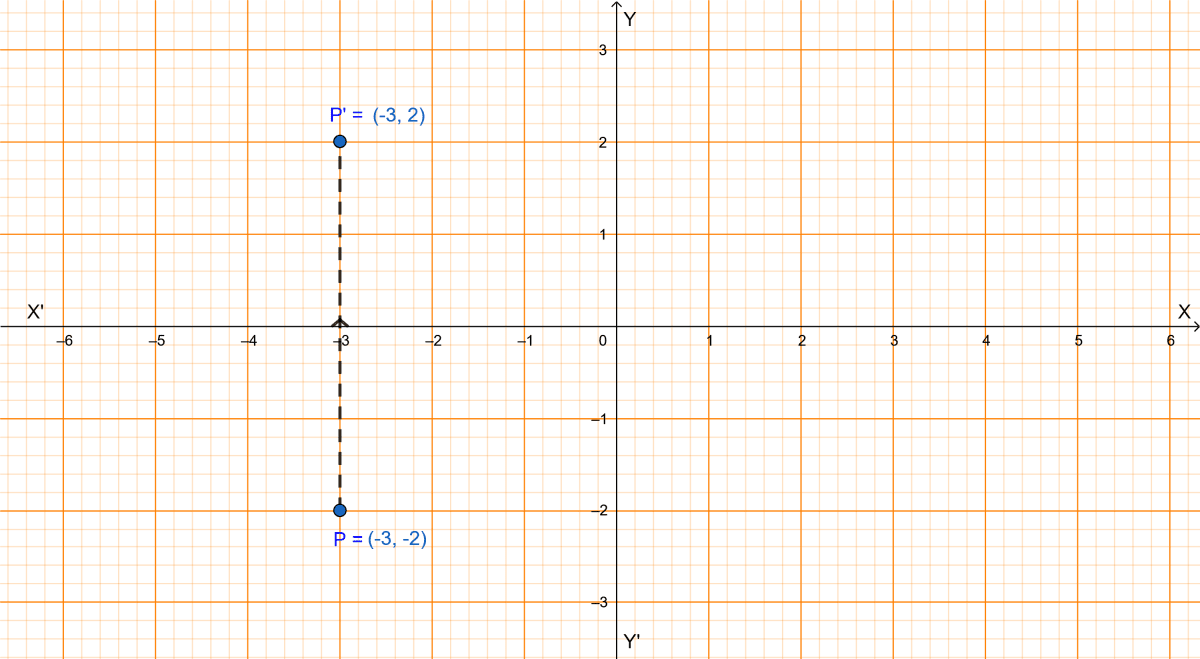
Hence, Option 2 is the correct option.

Question 4

The reflection of the point P(1, -2) in the line y = -1 is

1. (-3, -2)

2. (1, -4)

3. (1, 4)

4. (1, 0)

Answer

We know that the reflection of the point (x, y) in the line y = a is the point (x, -y + 2a).

∴ The image of the point P(1, -2) under reflection in the line y = -1 is the point (1, -(-2) + 2 × (-1)) i.e the point (1, 0).

Hence, Option 4 is the correct option.

Question 5

The reflection of the point A(4, -1) in the line x = 2 is

1. (0, -1)

2. (8, -1)

3. (0, 1)

4. none of these

Answer

We know that the reflection of the point (x, y) in the line x = a is the point (-x + 2a, y).

∴ The image of the point A(4, -1) under reflection in the line x = 2 is the point (-4 + 2 × 2, -1) i.e., the point P'(0, -1).

Hence, Option 1 is the correct option.

Question 6

The reflection of the point (-3, 0) in the origin is the point

1. (0, -3)

2. (0, 3)

3. (3, 0)

4. none of these

Answer

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Point (3, 0) is the image on reflection.

Hence, Option 3 is the correct option.

Question 7

Which of the following points is invariant with respect to the line y = -2?

1. (3, 2)

2. (3, -2)

3. (2, 3)

4. (-2, 3)

Answer

Since, in (3, -2), y = -2, it means this point lies on the line. Hence, it a invariant point.

Hence, Option 2 is the correct option.

Chapter Test

Question 1

The point P(4, -7) on reflection in x-axis is mapped onto P'. Then P' on reflection in the y-axis is mapped onto P''. Find the coordinates of P' and P''. Write down a single transformation that maps P onto P''.

Answer

We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of point P(4, -7) on reflection in x-axis is P'(4, 7).

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Coordinates of point P'(4, 7) on reflection in y-axis is P''(-4, 7).

The single transformation that maps P(4, -7) onto P''(-4, 7) is reflection in the origin.

Question 2

The point P(a, b) is first reflected in the origin and then reflected in the y-axis to P'. If P' has coordinates (3, -4), evaluate a, b.

Answer

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of point P(a, b) on reflection in origin is (-a, -b).

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Coordinates of point (-a, -b) on reflection in y-axis is (a, -b).

According to question after reflection in y-axis the point is P'(3, -4).

∴ (3, -4) = (a, -b) or, a = 3 and b = 4.

Hence, the value of a = 3, b = 4.

Question 3

A point P(a, b) become (-2, c) after reflection in the x-axis, and P becomes (d, 5) after reflection in the origin. Find the values of a, b, c and d.

Answer

We know that,

Rule to find reflection of a point in x-axis :

1. Retain the abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of point P(a, b) on reflection in x-axis is P'(a, -b).

According to question after reflection in x-axis P becomes (-2, c).

∴ (a, -b) = (-2, c) or,
⇒ a = -2
⇒ -b = c or b = -c.

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of point P(a, b) on reflection in origin is (-a, -b).

According to question after reflection in origin P becomes (d, 5).

∴ (-a, -b) = (d, 5) or,
⇒ -a = d or d = -(-2) = 2.
⇒ -b = 5 or b = -5.

Since, b = -c = -5, so, c = 5.

Hence, the value of a = -2, b = -5, c = 5 and d = 2.

Question 4

A(4, -1), B(0, 7) and C(-2, 5) are the vertices of a triangle. △ABC is reflected in the y-axis and then reflected in the origin. Find the coordinates of the final images of the vertices.

Answer

The graph for this problem is shown below:

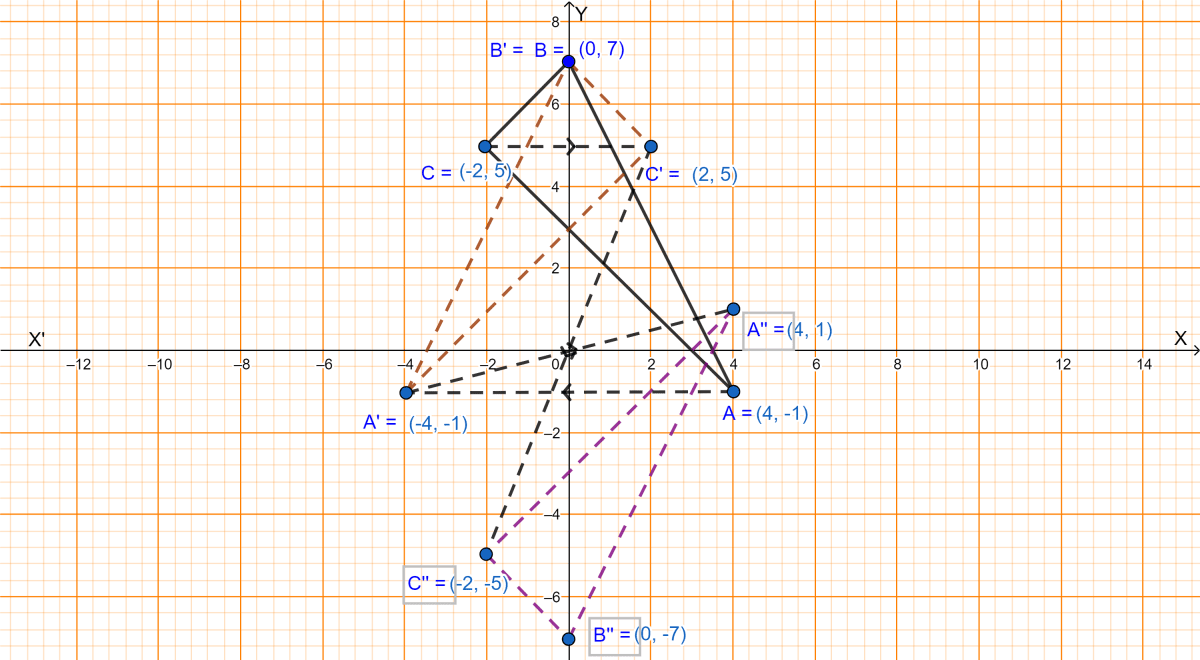
First the triangle is reflected in y-axis.

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Coordinates of
⇒ A(4, -1) on reflection in y-axis becomes A'(-4, -1).
⇒ B(0, 7) on reflection in y-axis becomes B'(0, 7).
⇒ C(-2, 5) on reflection in y-axis becomes C'(2, 5).

Now the triangle is reflected in origin.

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of
⇒ A'(-4, -1) on reflection in y-axis becomes A''(4, 1).
⇒ B'(0, 7) on reflection in y-axis becomes B''(0, -7).
⇒ C'(2, 5) on reflection in y-axis becomes C''(-2, -5).

Hence, the coordinates of the final images of the vertices are (4, 1), (0, -7) and (-2, -5) respectively.

Question 5

The points A(4, -11), B(5, 3), C(2, 15) and D(1, 1) are the vertices of a parallelogram. If the parallelogram is reflected in the y-axis and then in the origin, find the coordinates of the final images. Check whether it remains a parallelogram. Write down a single transformation that brings the above change.

Answer

The graph for this problem is shown below:

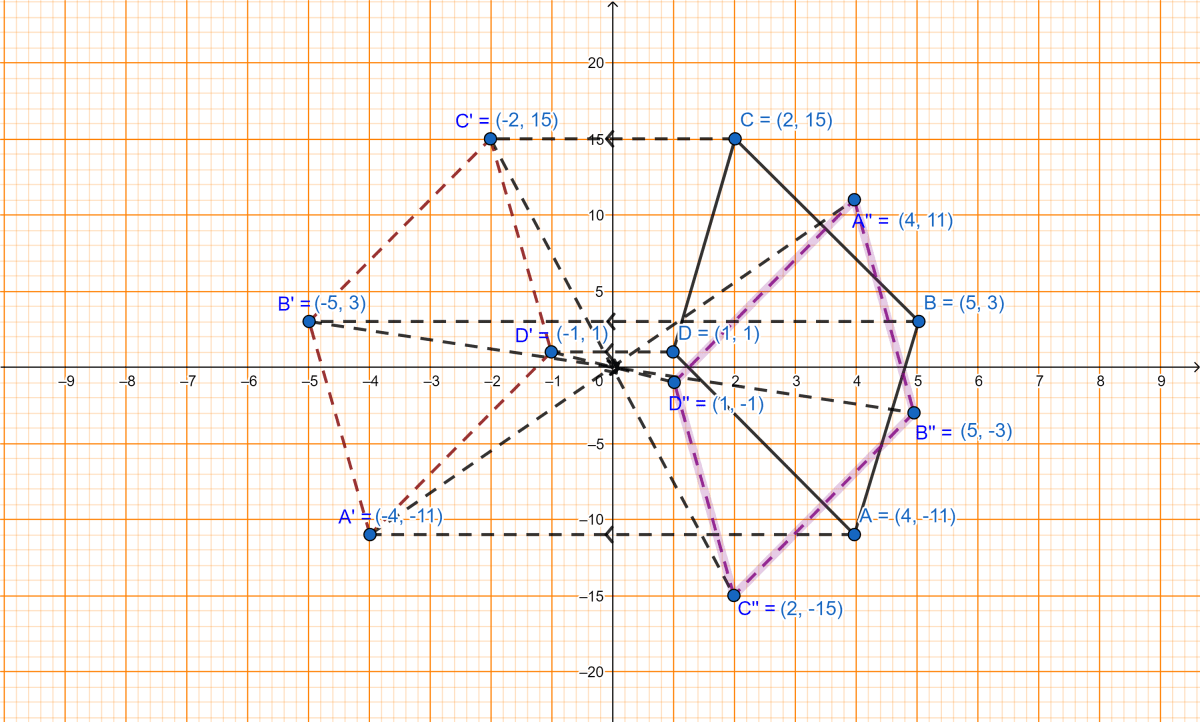
First the parallelogram is reflected in y-axis.

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

∴ Coordinates of
⇒ A(4, -11) on reflection in y-axis becomes A'(-4, -11).
⇒ B(5, 3) on reflection in y-axis becomes B'(-5, 3).
⇒ C(2, 15) on reflection in y-axis becomes C'(-2, 15).
⇒ D(1, 1) on reflection in y-axis becomes D'(-1, 1).

We know that,

Rules to find the reflection of a point in the origin :

1. Change the sign of abscissa i.e. x-coordinate.
2. Change the sign of ordinate i.e. y-coordinate.

∴ Coordinates of
⇒ A'(-4, -11) on reflection in origin becomes A''(4, 11).
⇒ B'(-5, 3) on reflection in origin becomes B''(5, -3).
⇒ C'(-2, 15) on reflection in origin becomes C''(2, -15).
⇒ D'(-1, 1) on reflection in origin becomes D''(1, -1)

From graph we can see that A"B"C"D" is also a parallelogram.

The single transformation that marks the following changes i.e.
A(4, -11) ⇒ A"(4, 11)
B(5, 3) ⇒ B"(5, -3)
C(2, 15) ⇒ C"(2, -15)
D(1, 1) ⇒ D"(1, -1), is reflection in x-axis.

Hence,

1. The coordinates of the final images of the vertices are (4, 11), (5, -3), (2, -15) and (1, -1) respectively.
2. These new images still form parallelogram.
3. The single transformation from ABCD ⇒ A"B"C"D" can be achieved by reflection in x-axis.

Question 6

Use a graph paper for this question (take 2 cm = 1 unit on both x and y axes).

(i) Plot the following points : A(0, 4), B(2, 3), C(1, 1) and D(2, 0).

(ii) Reflect points B, C, D on y-axis and write down their coordinates. Name the images as B', C', D' respectively.

(iii) Join points A, B, C, D, D', C', B' and A in order, so as to form a closed figure. Write down the equation of line of symmetry of the figure formed.

Answer

(i) The point A(0, 4), B(2, 3), C(1, 1) and D(2, 0) are plotted on the graph below:

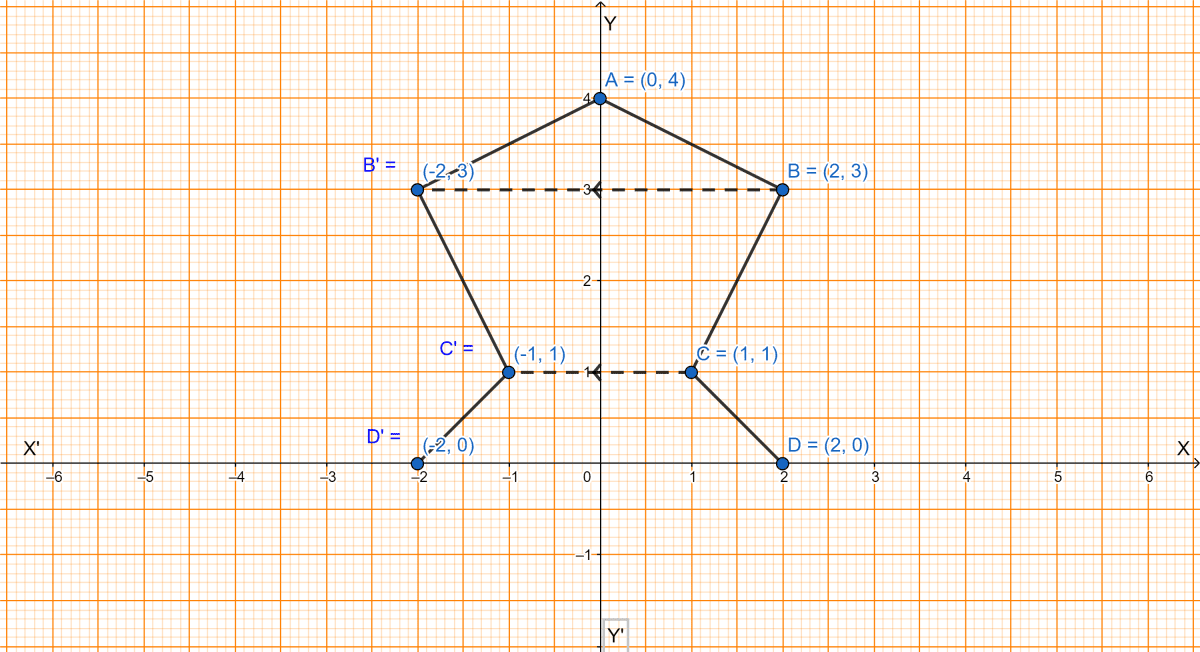
(ii) From graph, on reflecting B, C, D on y-axis we get,

     B(2, 3) ⇒ B'(-2, 3)
     C(1, 1) ⇒ C'(-1, 1)
     D(2, 0) ⇒ D'(-2, 0).

(iii) From graph we see that the figure is divided into two symmetrical parts by y-axis. Hence, the equation of line of symmetry is x = 0.

Question 7

The triangle OAB is reflected in the origin O to triangle triangle OA'B'. A' and B' have coordinates (-3, -4) and (0, -5) respectively.

(i) Find the coordinates of A and B.

(ii) Draw a diagram to represent the given information.

(iii) What kind of figure is the quadrilateral ABA'B'?

(iv) Find the coordinates of A'', the reflection of A in the origin followed by reflection in the y-axis.

(v) Find the coordinates of B'', the reflection of B in the x-axis followed by the reflection in the origin.

Answer

The graph showing the given information is drawn below:

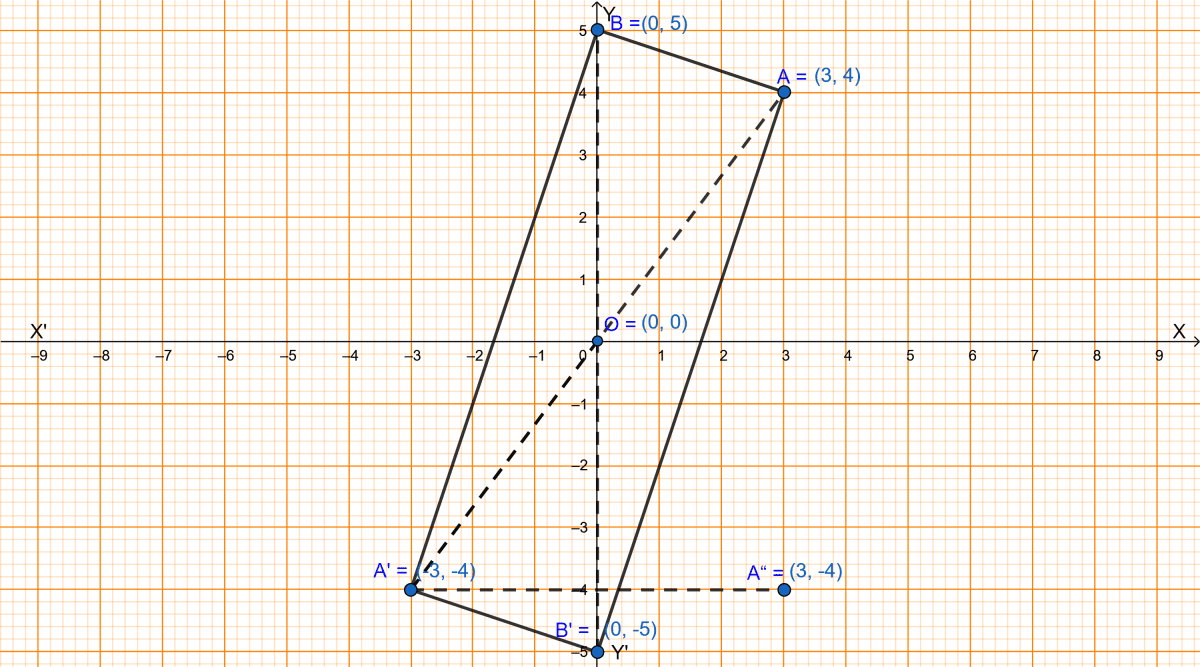
(i) Since, on reflection in the origin A becomes A'(-3, -4) and B becomes B'(0, -5) thus,

A = (3, 4) and B = (0, 5).

(iii) The quadrilateral ABA'B' represents a rectangle.

(iv) From graph we get,

The coordinates of A" is (3, -4).

(v) From graph we get,

The coordinates of B" is (0, 5).