Polynomials
The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
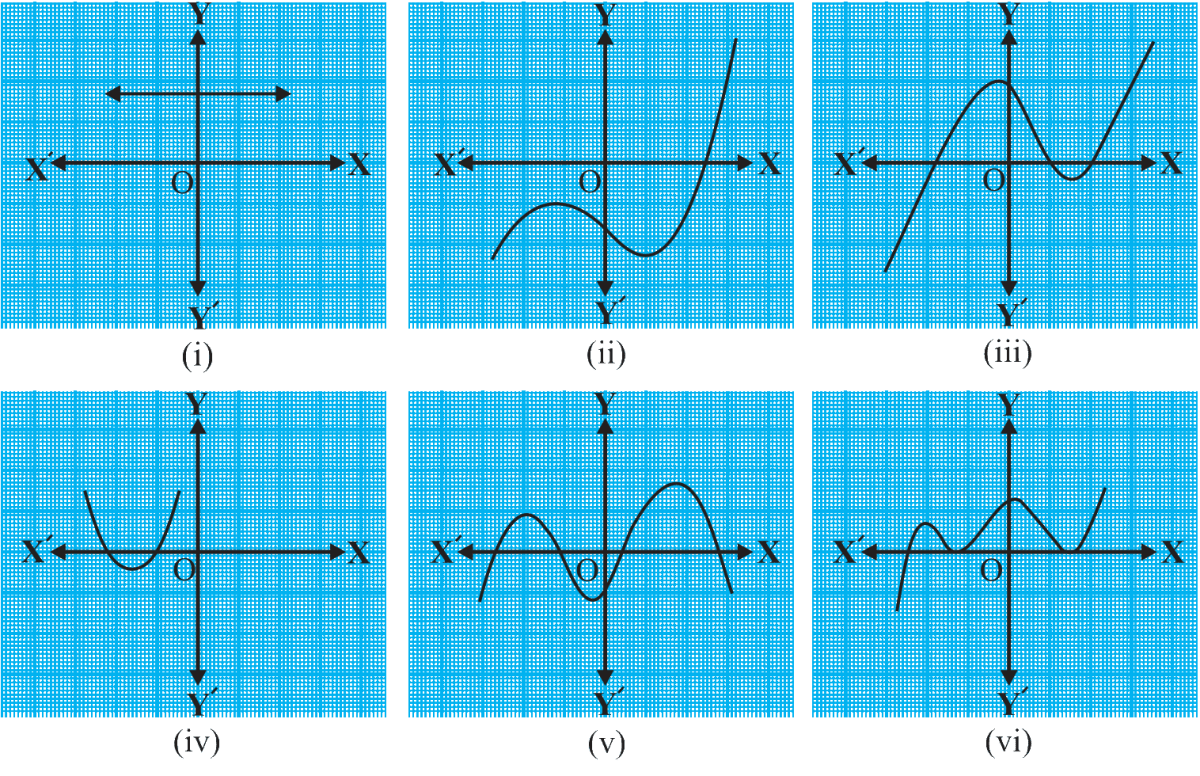
Answer
We know that,
The number of points where the graph cuts the x-axis gives the number of zeroes of any polynomial p(x).
(i) In the figure,
The graph does not cuts x-axis.
Hence, there are no zeroes in this graph.
(ii) In the figure,
The graph cuts x-axis at a single point.
Hence, there is one zero in this graph.
(iii) In the figure,
The graph cuts x-axis at three points.
Hence, there are three zeroes in this graph.
(iv) In the figure,
The graph cuts x-axis at two points.
Hence, there are two zeroes in this graph.
(v) In the figure,
The graph cuts x-axis at four points.
Hence, there are four zeroes in this graph.
(vi) In the figure,
The graph cuts x-axis at three points.
Hence, there are three zeroes in this graph.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
x2 - 2x - 8
Answer
Let,
⇒ x2 - 2x - 8 = 0
⇒ x2 - 4x + 2x - 8 = 0
⇒ x(x - 4) + 2(x - 4) = 0
⇒ (x + 2)(x - 4) = 0
⇒ x + 2 = 0 or x - 4 = 0
⇒ x = -2 or x = 4.
Sum of zeroes = (-2) + 4 = 2 = .
Product of zeroes = -2 × 4 = -8 =
Hence, for zero of the polynomial x2 - 2x - 8, x = -2, 4.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
4s2 - 4s + 1
Answer
Let,
⇒ 4s2 - 4s + 1 = 0
⇒ 4s2 - 2s - 2s + 1 = 0
⇒ 2s(2s - 1) - 1(2s - 1) = 0
⇒ (2s - 1)(2s - 1) = 0
⇒ (2s - 1)= 0 or (2s - 1) = 0
⇒ 2s = 1 or 2s = 1
⇒ s = or s = .
Sum of the zeroes = .
Product of zeroes =
Hence, for zero of the polynomial 4g2 - 4g + 1, g = .
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
6x2 - 3 - 7x
Answer
Let,
⇒ 6x2 - 3 - 7x = 0
⇒ 6x2 - 7x - 3 = 0
⇒ 6x2 - 9x + 2x - 3 = 0
⇒ 3x(2x - 3) + 1(2x - 3) = 0
⇒ (3x + 1)(2x - 3) = 0
⇒ 3x + 1 = 0 or 2x - 3 = 0
⇒ 3x = -1 or 2x = 3
⇒ x = or x =
Sum of zeroes =
Product of zeroes =
Hence, for zero of the polynomial 6x2 - 3 - 7x, x = .
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
4u2 + 8u
Answer
Let,
⇒ 4u2 + 8u = 0
⇒ 4u(u + 2) = 0
⇒ 4u = 0 or u + 2 = 0
⇒ u = 0 or u = -2.
Sum of zeroes = 0 + (-2) = -2 =
Product of zeroes = 0 × (-2) = 0 =
Hence, for zero of the polynomial 4u2 + 8u, u = 0, -2.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
t2 - 15
Answer
Let,
⇒ t2 - 15 = 0
⇒
⇒
⇒
Sum of zeroes =
Product of zeroes =
Hence, for zero of the polynomial t2 - 15, t = .
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
3x2 - x - 4
Answer
Let,
⇒ 3x2 - x - 4 = 0
⇒ 3x2 - 4x + 3x - 4 = 0
⇒ x(3x - 4) + 1(3x - 4) = 0
⇒ (x + 1)(3x - 4) = 0
⇒ x + 1 = 0 or 3x - 4 = 0
⇒ x = -1 or 3x = 4
⇒ x = -1 or x = .
Sum of zeroes =
Product of zeroes = .
Hence, for zero of the polynomial 3x2 - x - 4 = 0, x = -1, .
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Answer
For given roots,
Quadratic equation : x2 - (Sum of roots)x + (Product of roots) = 0
Substituting values we get :
Hence, required quadratic equation is 4x2 - x - 4 = 0.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Answer
For given roots,
Quadratic equation : x2 - (Sum of roots)x + (Product of roots) = 0
Substituting values we get :
Hence, required quadratic equation is .
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Answer
For given roots,
Quadratic equation : x2 - (Sum of roots)x + (Product of roots) = 0
Substituting values we get :
Hence, required quadratic equation is
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
1, 1
Answer
For given roots,
Quadratic equation : x2 - (Sum of roots)x + (Product of roots) = 0
Substituting values we get :
⇒ x2 - 1x + 1 = 0
⇒ x2 - x + 1 = 0.
Hence, required quadratic equation is x2 - x + 1 = 0.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(vi) 4, 1
Answer
For given roots,
Quadratic equation : x2 - (Sum of roots)x + (Product of roots) = 0
Substituting values we get :
Hence, required quadratic equation is 4x2 + x + 1 = 0.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
4, 1
Answer
(vi) For given roots,
Quadratic equation : x2 - (Sum of roots)x + (Product of roots) = 0
Substituting values we get :
⇒ x2 - 4x + 1 = 0
Hence, required quadratic equation is x2 - 4x + 1 = 0.