Proofs in Mathematics
State whether the following statements are always true, always false or ambiguous. Justify your answers.
(i) There are 13 months in a year.
(ii) Diwali falls on a Friday.
(iii) The temperature in Magadi is 26°C.
(iv) The earth has one moon.
(v) Dogs can fly.
(vi) February has only 28 days.
Answer
(i) This statement is always false, as there are 12 months in a year.
(ii) This statement is ambigious, because it is not necessary that Diwali falls on a Friday every year.
(iii) This statement is ambiguous, because temperature does not remains fixed. At some time in the year, the temperature in Magadi, could be less than or greater than 26°C.
(iv) This statement is always true, because the earth has only one moon.
(v) This statement is always false, because dogs cannot fly.
(vi) This statement is ambiguous, because in a leap year, February has 29 days and in non-leap years February has 28 days.
State whether the following statements are true or false. Give reasons for your answers.
(i) The sum of the interior angles of a quadrilateral is 350°.
(ii) For any real number x, x2 ≥ 0.
(iii) A rhombus is a parallelogram.
(iv) The sum of two even numbers is even.
(v) The sum of two odd numbers is odd.
Answer
(i) This statement is false because the sum of the interior angles of a quadrilateral is 360°.
(ii) This statement is true for all real numbers (x), x2 ≥ 0.
(iii) This statement is true because in a rhombus, both pairs of opposite sides are parallel and hence every rhombus is a parallelogram.
(iv) This statement is true because this is true for any two even numbers.
(v) This statement is false because the sum of any two odd numbers is always an even number.
Restate the following statements with appropriate conditions, so that they become true statements.
(i) All prime numbers are odd.
(ii) Two times a real number is always even.
(iii) For any x, 3x + 1 > 4.
(iv) For any x, x3 ≥ 0.
(v) In every triangle, a median is also an angle bisector.
Answer
(i) We know that,
A natural number that has exactly two factors, i.e., 1 and the number itself, is a prime number. Example - 2, 3, 5, 7,.......
Hence, all prime numbers greater than 2 are odd.
(ii) Let real number be 1.5
On multiplying by 2, we get :
1.5 × 2 = 3, which is an odd number.
∴ The statement, two times a real number is always even, is incorrect.
But if we multiply, any natural number by 2, we always get an even number.
Hence, two times a natural number is always even.
(iii) Given,
⇒ 3x + 1 > 4
⇒ 3x > 4 - 1
⇒ 3x > 3
⇒ x >
⇒ x > 1.
Hence, for x > 1, 3x + 1 > 4.
(iv) For any x ≥ 0, x3 ≥ 0.
(v) We know that,
A median is also the angle bisector in equilateral triangle.
Hence, in equilateral triangle, a median is also an angle bisector.
Use deductive reasoning to answer the following:
(i) Humans are mammals. All mammals are vertebrates. Based on these two statements, what can you conclude about humans?
(ii) Anthony is a barber. Dinesh had his hair cut. Can you conclude that Antony cut Dinesh’s hair?
(iii) Martians have red tongues. Gulag is a Martian. Based on these two statements, what can you conclude about Gulag?
(iv) If it rains for more than four hours on a particular day, the gutters will have to be cleaned the next day. It has rained for 6 hours today. What can we conclude about the condition of the gutters tomorrow?
(v) What is the fallacy in the cow’s reasoning in the cartoon below?

Answer
(i) Since, all humans are mammals and all mammals are vertebrates.
∴ We can conclude that,
Humans are vertebrates.
(ii) Since, Anthony is a barber and Dinesh had his hair cut.
∴ We can conclude that,
It is not necessary that Antony has cut Dinesh’s hair, as Dinesh could have got his hair cut by another barber.
(iii) Since, Martians have red tongues and Gulag is a Martian.
∴ We can conclude that,
Gulag has a red tongue.
(iv) Given,
If it rains for more than four hours on a particular day, the gutters will have to be cleaned the next day and it has rained for 6 hours today.
∴ We can conclude that,
The gutters will have to be cleaned tomorrow.
(v) We know that,
All animals have tails need not be dogs. For example, animals such as buffaloes, monkeys, cats, etc. have tails but are not dogs.
Once again you are given four cards. Each card has a number printed on one side and a letter on the other side. Which are the only two cards you need to turn over to check whether the following rule holds?
"If a card has a consonant on one side, then it has an odd number on the other side."
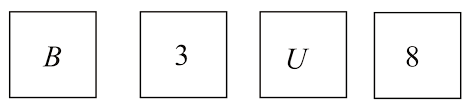
Answer
We need to turn over B and 8, in order to check whether the rule holds.
Rule is broken, if any of the one condition occurs :
If B has an even number on the other side.
If 8 has a consonant on the other side.
Take any three consecutive even numbers and find their product; for example, 2 × 4 × 6 = 48, 4 × 6 × 8 = 192, and so on. Make three conjectures about these products.
Answer
Let three consecutive numbers be 8, 10 and 12.
Product = 8 × 10 × 12 = 960.
Three possible conjectures are:
(i) The product of any three consecutive even numbers is even.
(ii) The product of any three consecutive even numbers is divisible by 4.
(iii) The product of any three consecutive even numbers is divisible by 6.
Go back to Pascal’s triangle.
Line 1 : 1 = 110
Line 2 : 1 1 = 111
Line 3 : 1 2 1 = 112
Make a conjecture about Line 4 and Line 5. Does your conjecture hold? Does your conjecture hold for Line 6 too?
Answer
Given,
Line 1 : 1 = 110
Line 2 : 1 1 = 111
Line 3 : 1 2 1 = 112
Looking at the above pascal triangle,
Possible conjecture :
Line 4
1 3 3 1 = 113
Line 5
1 4 6 4 1 = 114
Since, The conjecture holds for line 4 and line 5.
Line 6 :
161051 = 115
The conjecture does not holds for above line.
Hence, conjecture holds for line 4 and 5 but does not holds for line 6.
Let us look at the triangular numbers figure again. Add two consecutive triangular numbers. For example, T1 + T2 = 4, T2 + T3 = 9, T3 + T4 = 16.
What about T4 + T5 ? Make a conjecture about Tn-1 + Tn.
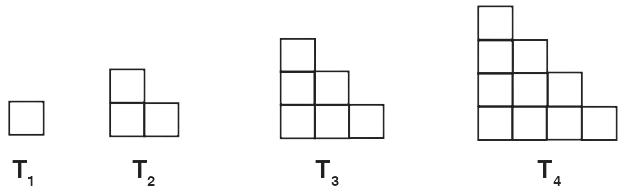
Answer
Given,
⇒ T1 + T2 = 4 = 22
⇒ T2 + T3 = 9 = 32
⇒ T3 + T4 = 16 = 42
Conjecture :
On adding two triangular numbers the resultant value is the square of the larger number.
By using conjecture :
⇒ T4 + T5 = 52 = 25.
Hence, Tn - 1 + Tn = n2.
Look at the following pattern :
12 = 1
112 = 121
1112 = 12321
11112 = 1234321
111112 = 123454321
Make a conjecture about each of the following:
1111112 =
11111112 =
Check if your conjecture is true.
Answer
Looking at above pattern,
Possible conjecture :
The resultant will be series of numbers from one till number of 1's in the digit to be squared and then reversing the order.
By following conjecture, we can write:
⇒ 1111112 = 12345654321 and
⇒ 11111112 = 1234567654321
On actual multiplication, we get :
⇒ 1111112 = 12345654321 and
⇒ 11111112 = 1234567654321.
Hence, conjecture is true.
List five axioms (postulates) used in this book.
Answer
Euclid's postulates are:
Axiom 5.1- Things which are equal to the same thing are equal to one another.
Axiom 5.2 - If equals are added to equals, the wholes are equal.
Axiom 5.3 - If equals are subtracted from equals, the remainders are equal.
Axiom 5.4 - Things which coincide with one another are equal to one another.
Axiom 5.5 - The whole is greater than the part.
Find counter-examples to disprove the following statements:
(i) If the corresponding angles in two triangles are equal, then the triangles are congruent.
(ii) A quadrilateral with all sides equal is a square.
(iii) A quadrilateral with all angles equal is a square.
(iv) For integers a and b, = a + b
(v) 2n2 + 11 is a prime for all whole numbers n.
(vi) n2 – n + 41 is a prime for all positive integers n.
Answer
(i) Counter example :
Consider two equilateral triangle Δ ABC and Δ DEF of length 3 cm and 6 cm respectively.
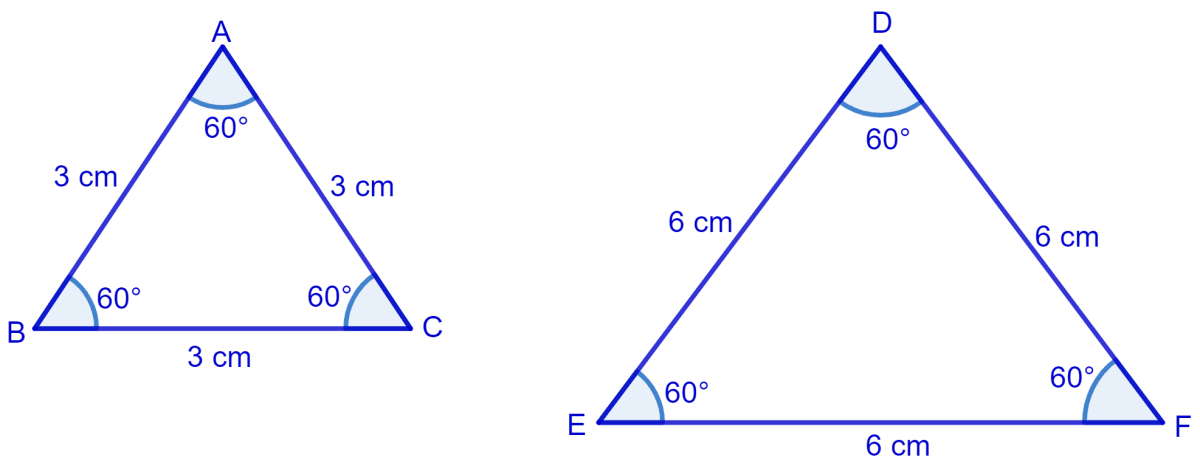
From figure,
All corresponding angles are same but sides are of different length.
∴ Δ ABC and Δ DEF are not congruent.
(ii) Counter example :
A quadrilateral with all sides equal is a rhombus which may not be a square.
(iii) Counter example :
A rectangle has all angles equal, but may not be a square.
(iv) Given,
Equation : = a + b
Counter example : Let a = 3 and b = 4
Substituting value of a and b in L.H.S. of the equation, we get :
Substituting value of a and b in R.H.S. of the equation, we get :
⇒ 3 + 4 = 7.
Since,
L.H.S. ≠ R.H.S.
Hence, for a = 3 and b = 4, the statement = a + b is not true.
(v) Given,
Equation : 2n2 + 11
Counter example :
Let n = 11 (by hit and trial method)
Substituting value of n in given equation.
2n2 + 11 = 2(11)2 + 11
= 2 x 121 + 11
= 242 + 11 = 253.
253 is divisible by 11.
Therefore, 253 is not a prime number so given statement is false for n = 11.
Hence, for n = 11, 2n2 + 11 = 253, which is not a prime number.
(vi) Given,
Equation : n2 - n + 41
Counter example :
Let n = 41.
Substituting value of n in given equation, we get :
n2 - n + 41 = (41)2 - 41 + 41
= 1681.
1681 is not prime.
Hence, for n = 41, n2 – n + 41 is not prime.
Take your favourite proof and analyse it step-by-step along the lines discussed in Section A1.5 (what is given, what has been proved, what theorems and axioms have been used, and so on).
Answer
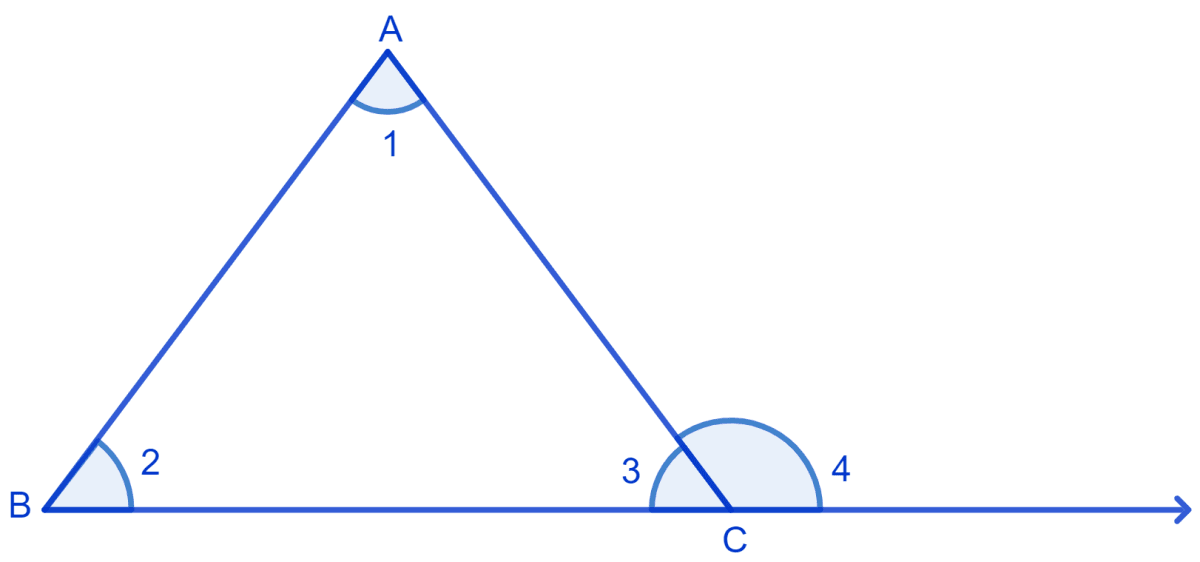
If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
In Δ ABC,
⇒ ∠1 + ∠2 + ∠3 = 180° (By angle sum property) .....(1)
⇒ ∠3 + ∠4 = 180° (Linear pair) ....(2)
By comparing equation (1) and (2), we get :
⇒ ∠1 + ∠2 + ∠3 = ∠3 + ∠4
⇒ ∠1 + ∠2 = ∠4
Hence, proved that if a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
Analysis of proof :
We begin with a triangle and one exterior angle.
Here we use angle sum property of triangle that is sum of three interior angles of a triangle is 180° to show ∠1 + ∠2 + ∠3 = 180°.(By theorem)
Here we use linear pair axiom, which states that the angles on a straight line add up to 180° to show that ∠3 + ∠4 = 180°.
Here we use Euclid's axiom which states that: “Things which are equal to the same thing are equal to each other.”
Here we use Euclid‟s axiom which states that: “If equals are subtracted from equals, the remainders are equal.”
Prove that the sum of two odd numbers is even.
Answer
Let x and y be two odd numbers.
Then x = 2k + 1 for some natural number and y = 2l + 1 for some natural number l.
Adding x and y, we get :
⇒ x + y = 2k + 1 + 2l + 1
= 2k + 2l + 2
= 2(k + l + 1).
We know that,
Any natural number on multiplying by 2 is an even number.
Hence, proved that the sum of two odd numbers is even.
Prove that the product of two odd numbers is odd.
Answer
Let x and y be two odd numbers.
Then x = 2k + 1 for some natural number k and y = 2l + 1 for some natural number l.
Multipying both x and y, we get :
⇒ xy = (2k + 1)(2l + 1)
⇒ xy = 2k(2l + 1) + 1(2l + 1)
⇒ xy = 4kl + 2k + 2l + 1
⇒ xy = 2(kl + k + l) + 1
Let (kl + l + 1) be M.
⇒ xy = 2M + 1
We know that,
Any natural number on multiplying by 2 is an even number.
On adding 1 to an even number we an odd number.
So, product of two odd numbers is odd.
Hence, proved that the product of two odd numbers is odd.
Prove that the sum of three consecutive even numbers is divisible by 6.
Answer
Let three consecutive even numbers be : 2n, 2n + 2, 2n + 4
Their sum = 2n + 2n + 2 + 2n + 4
⇒ (2n + 2n + 2n) + (2 + 4)
⇒ 6n + 6 = 6(n + 1) = 6k, where k = n + 1.
Clearly 6k is divisible by 6.
Hence, proved that the sum of three consecutive even numbers is divisible by 6.
Prove that infinitely many points lie on the line whose equation is y = 2x. (Hint : Consider the point (n, 2n) for any integer n.)
Answer
Consider the point (n, 2n) for any integer n.
Given equation y = 2x ....(1)
Putting x = n and y = 2n in equation (1) we get :
⇒ 2n = 2(n)
⇒ 2n = 2n, which is always true.
So, (n, 2n) lies on equation (1).
Now for infinite values of n, we can obtain infinite points which lie on line whose equation is y = 2x.
Hence, proved that infinitely many points lie on the line whose equation is y = 2x.
You must have had a friend who must have told you to think of a number and do various things to it, and then without knowing your original number, telling you what number you ended up with. Here are two examples. Examine why they work.
(i) Choose a number. Double it. Add nine. Add your original number. Divide by three. Add four. Subtract your original number. Your result is seven.
(ii) Write down any three-digit number (for example, 425). Make a six-digit number by repeating these digits in the same order (425425). Your new number is divisible by 7, 11 and 13.
Answer
(i) Steps :
Let our original number be n.
Double the number (2n).
Add nine to the number (2n + 9).
Add original number (2n + 9 + n = 3n + 9).
Divide the number by 3 = = n + 3.
Add four (n + 3 + 4 = n + 7).
Subtract original number (n + 7 - n = 7).
From above steps,
It is clear that on selecting any number, the answer remain same, i.e., 7.
(ii) Multiplying 7, 11 and 13 we get :
7 x 11 x 13 = 1001
Take any three digits number say, xyz.
On multiplying,
⇒ xyz x 1001 = xyzxyz
Since, 7, 11 and 13 are factor of 1001 and 1001 is a factor of xyzxyz.
∴ 7, 11 and 13 are factor of xyzxyz.
Hence, any six digit number of form xyzxyz formed from a three digit number of form xyz is divisible by 7, 11 and 13.