Multiple-Choice Questions
A retailer buys an article at its listed price from a wholesaler and sells it to a consumer in the same state after marking up the price by 20%. The list price of the article is ₹ 2500, and the rate of GST is 12%. What is the tax liability of the retailer to the central government?
₹ 0
₹ 15
₹ 30
₹ 60
Answer
For retailer,
C.P. = ₹ 2500
G.S.T. = 12%
C.G.S.T. = % = 6%.
C.G.S.T. paid = = ₹ 150.
Given,
Retailer sells the article to the consumer in the same state after marking up the price by 20%.
S.P. = ₹ 2500 + 20%
= ₹ 2500 +
= ₹ 2500 + ₹ 500
= ₹ 3000.
C.G.S.T. = 6%
C.G.S.T. charged = = ₹ 180.
Tax liability = C.G.S.T. charged - C.G.S.T. given
= ₹ 180 - ₹ 150
= ₹ 30.
Hence, Option 3 is the correct option.
Dev brought an electrical fan which has a marked price of ₹ 800. If the GST on the goods is 7%, then the SGST is :
₹ 24
₹ 28
₹ 56
₹ 80
Answer
Since, GST rate is 7%, then SGST = = 3.5%.
M.P. of electrical fan = ₹ 800.
SGST = 3.5% of ₹ 800
=
= ₹ 28.
Hence, Option 2 is the correct option.
₹ P is deposited for n number of months in a recurring deposit account which pays interest at the rate of r% per annum. The nature and time of interest calculated is :
compound interest for n number of months
simple interest for n number of months
compound interest for one month
simple interest for one month
Answer
In a recurring deposit account,
By formula,
Interest =
∴ The nature and time of interest calculated is simple interest for one month.
Hence, Option 4 is the correct option.
Anwesha intended to open a Recurring Deposit account of ₹ 1000 per month for 1 year in a Bank, paying a 5% per annum rate of simple interest. The bank reduced the rate to 4% per annum. How much must Anwesha deposit monthly for 1 year so that her interest remains the same?
₹ 12325
₹ 1250
₹ 1200
₹ 1000
Answer
In first case :
P = ₹ 1000
r = 5%
n = 12 months
Interest =
In second case :
P = ₹ x (Let)
r = 4%
n = 12 months
Interest = ₹ 325
Hence, Option 2 is the correct option.
Mr. Das invests in ₹ 100, 12% shares of Company A available at ₹ 60 each. Mr. Singh invests in ₹ 50, 16% shares of Company B available at ₹ 40 each. Use this information to state which of the following statements is true.
The rate of return for Mr. Das is 12%
The rate of return for Mr. Singh is 10%
Both Mr. Das and Mr. Singh have the same rate of return of 10%
Both Mr. Das and Mr. Singh have the same rate of return of 20%
Answer
For Mr. Das,
Face value of each share = ₹ 100
Market value of each share = ₹ 60
Dividend per share = 12% of ₹ 100 = ₹ 12.
Rate of return = = 20%.
For Mr. Singh,
Face value of each share = ₹ 50
Market value of each share = ₹ 40
Dividend per share = 16% of ₹ 50 = ₹ 8.
Rate of return = = 20%.
∴ Both Mr. Das and Mr. Singh have the same rate of return of 20%.
Hence, Option 4 is the correct option.
Amit invested a certain sum of money in ₹ 100 shares, paying a 7.5% dividend. The rate of return on his investment is 10%. The money invested by Amit to purchase 10 shares is :
₹ 250
₹ 750
₹ 900
₹ 1100
Answer
Let ₹ P be the price per share.
Amit brought 10 shares, so total investment = ₹ 10P
Dividend = 7.5%
Dividend per share = = ₹ 7.5
Total dividend = ₹ 7.5 × 10 = ₹ 75.
Rate of return = 10%
By formula,
Rate of return × Investment = Dividend
Total investment = 10P = 10 × ₹75 = ₹750.
Hence, Option 2 is the correct option.
If -3 ≤ -4x + 5 and x ∈ W, then the solution set is :
{.......-3, -2, -1, 0, 1, 2, 3, .......}
{1, 2}
{0, 1, 2}
{2, 3, 4, 5}
Answer
Solving,
⇒ -3 ≤ -4x + 5
⇒ 4x ≤ 5 + 3
⇒ 4x ≤ 8
⇒ x ≤
⇒ x ≤ 2.
Since, x ≤ 2 and x ∈ W.
∴ Solution set = {0, 1, 2}.
Hence, Option 3 is the correct option.
If -4x > 8y; then
x > 2y
x > -2y
x < -2y
x < 2y
Answer
Solving,
⇒ -4x > 8y
⇒ 4x < -8y
⇒ x <
⇒ x < -2y.
Hence, Option 3 is the correct option.
The value/s of 'k' for which the quadratic equation 2x2 - kx + k = 0 has equal roots is (are) :
0 only
4, 0
8 only
0, 8
Answer
Given,
Equation : 2x2 - kx + k = 0
a = 2, b = -k and c = k.
For equal roots,
⇒ Discriminant (D) = 0
⇒ b2 - 4ac = 0
⇒ (-k)2 - 4 × 2 × k = 0
⇒ k2 - 8k = 0
⇒ k(k - 8) = 0
⇒ k = 0 or k - 8 = 0
⇒ k = 0 or k = 8.
Hence, Option 4 is the correct option.
If x = -2 is one of the solutions of the quadratic equation x2 + 3a - x = 0, then the value of 'a' is :
-8
-2
Answer
Given,
x = -2 is one of the solutions of the quadratic equation x2 + 3a - x = 0.
∴ (-2)2 + 3a - (-2) = 0
⇒ 4 + 3a + 2 = 0
⇒ 3a + 6 = 0
⇒ 3a = -6
⇒ a = = -2.
Hence, Option 2 is the correct option.
In solving a quadratic equation, one of the values of the variables x is 233.356. The solution rounded to two significant figures is :
233.36
233.35
233.3
230
Answer
x = 233.356
On rounding off to two significant figures
x = 230.
Hence, Option 4 is the correct option.
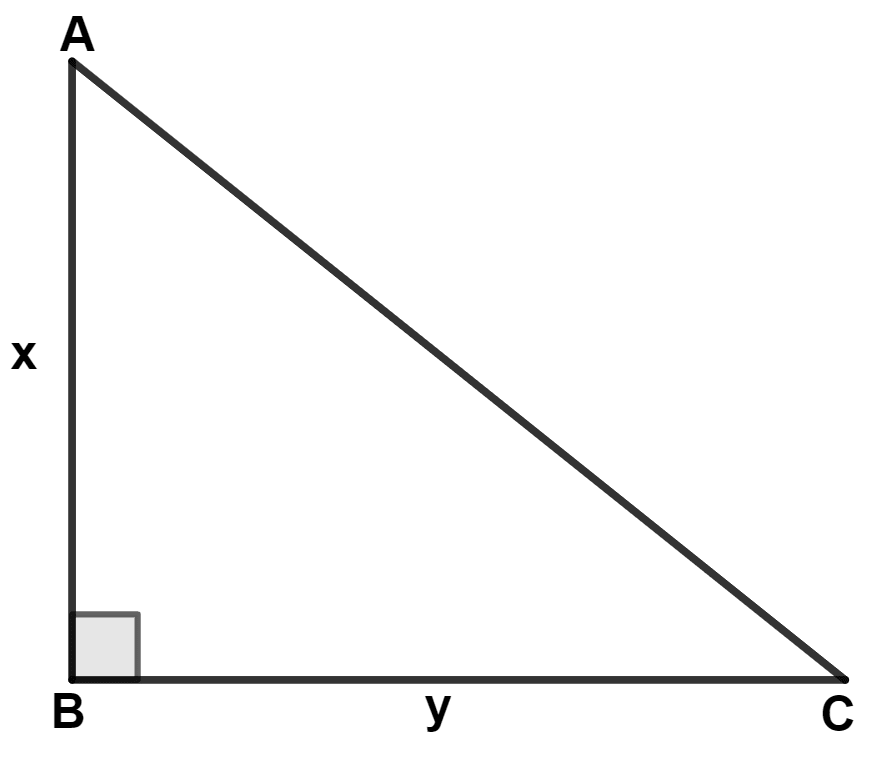
In the adjoining diagram, AB = x cm, BC = y cm and x - y = 7 cm. Area of △ ABC = 30 cm2. The length of AC is :
10 cm
12 cm
13 cm
15 cm
Answer
By formula,
Area of triangle =
⇒ 30 =
⇒ 30 =
⇒ 30 =
⇒ xy = 60 ........(1)
Given,
⇒ x - y = 7
⇒ x = 7 + y ........(2)
Substituting value of x from equation (2) in (1), we get :
⇒ (7 + y)y = 60
⇒ 7y + y2 = 60
⇒ y2 + 7y - 60 = 0
⇒ y2 + 12y - 5y - 60 = 0
⇒ y(y + 12) - 5(y + 12) = 0
⇒ (y - 5)(y + 12) = 0
⇒ y - 5 = 0 or y + 12 = 0
⇒ y = 5 or y = -12.
Since, side cannot be negative,
∴ y = 5 cm.
Substituting value of y in equation (2), we get :
⇒ x = 7 + y = 7 + 5 = 12 cm.
In right angle triangle ABC,
By pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = x2 + y2
⇒ AC2 = 122 + 52
⇒ AC2 = 144 + 25
⇒ AC2 = 169
⇒ AC = = 13 cm.
Hence, Option 3 is the correct option.
If p, q, and r are in continued proportion, then :
p : q = p : r
q : r = p2 : q2
p : q2 = r : p2
p : r = p2 : q2
Answer
Since, p, q, and r are in continued proportion.
Solving,
p : r = p2 : q2
Since, equation (1) and (2) are equal.
Hence, Option 4 is the correct option.
The ratio of diameter to height of a Borosil cylindrical glass is 3 : 5. If the actual diameter of the glass is 6 cm, then the curved surface area of the glass is :
120π
60π
30π
18π
Answer
Given,
Ratio of diameter to height of a Borosil cylindrical glass is 3 : 5.
Radius = = 3 cm.
By formula,
Curved surface area of glass = 2πrh
= 2π × 3 × 10
= 60π cm2.
Hence, Option 2 is the correct option.
If the polynomial 2x3 + 3x2 - 2x - 3 is completely divisible by (2x + a), and the quotient is equal to (x2 - 1), then one of the values of a is :
-3
-1
1
3
Answer
Given,
The polynomial 2x3 + 3x2 - 2x - 3 is completely divisible by (2x + a) and quotient is equal to (x2 - 1).
∴ 2x3 + 3x2 - 2x - 3 = (2x + a)(x2 - 1)
⇒ 2x3 + 3x2 - 2x - 3 = 2x3 - 2x + ax2 - a
⇒ 2x3 - 2x3 + 3x2 - 2x + 2x - 3 = ax2 - a
⇒ 3x2 - 3 = ax2 - a
From above equation,
a = 3.
Hence, Option 4 is the correct option.
A polynomial in x is x3 + 5x2 - kx - 24. Which of the following is a factor of the given polynomial so that the value of k is 2?
(x + 2)
(x - 3)
(x + 4)
(x - 4)
Answer
By factor theorem,
(x - a) is a factor of f(x), if f(a) = 0.
Given,
Polynomial = x3 + 5x2 - kx - 24
If k = 2, then :
Polynomial = x3 + 5x2 - 2x - 24.
Dividing polynomial by (x + 4) or substituting -4 in polynomial, we get :
⇒ (-4)3 + 5(-4)2 - 2(-4) - 24
⇒ -64 + 5(16) + 8 - 24
⇒ -64 + 80 + 8 - 24
⇒ 88 - 88
⇒ 0.
Since, on substituting -4 in polynomial, we get remainder = 0.
∴ (x + 4) is the factor of x3 + 5x2 - kx - 24, when k = 2.
Hence, Option 3 is the correct option.
If A = , then :
only matrix AB is possible
only matrix BA is possible
both matrices AB and BA are possible
both matrices AB and BA are possible, AB = BA
Answer
Order of matrix A = 1 × 2
Order of matrix B = 2 × 1
Since, no. of columns in A is equal to the no. of rows in B and no. of columns in B is equal to the no. of rows in A.
∴ AB and BA are possible.
∴ AB ≠ BA.
Hence, Option 3 is the correct option.
Matrix A = . Then k is :
6
-6
36
±6
Answer
Given, .
Hence, Option 2 is the correct option.
If the sum of n terms of an arithmetic progression Sn = n2 - n, then the third term of the series is :
2
4
6
9
Answer
Given,
Sum of n terms of an arithmetic progression Sn = n2 - n.
S1 = 12 - 1 = 0,
S2 = 22 - 2 = 4 - 2 = 2,
S3 = 32 - 3 = 9 - 3 = 6.
Sum upto first term = First term = 0.
Given, sum upto 2 terms = 2 and first term = 0, second term = 2.
Sum upto third term = 6
∴ First term + Second term + Third term = 6
⇒ 0 + 2 + Third term = 6
⇒ Third term = 6 - 2 = 4.
Hence, Option 2 is the correct option.
Which of the following is not a geometric progression ?
-2, 4, -8, 16
2, 0, 4, 0, 8, 0
Answer
In the series,
2, 0, 4, 0, 8, 0
∴ 2, 0, 4, 0, 8, 0 is not a G.P.
Hence, Option 4 is the correct option.
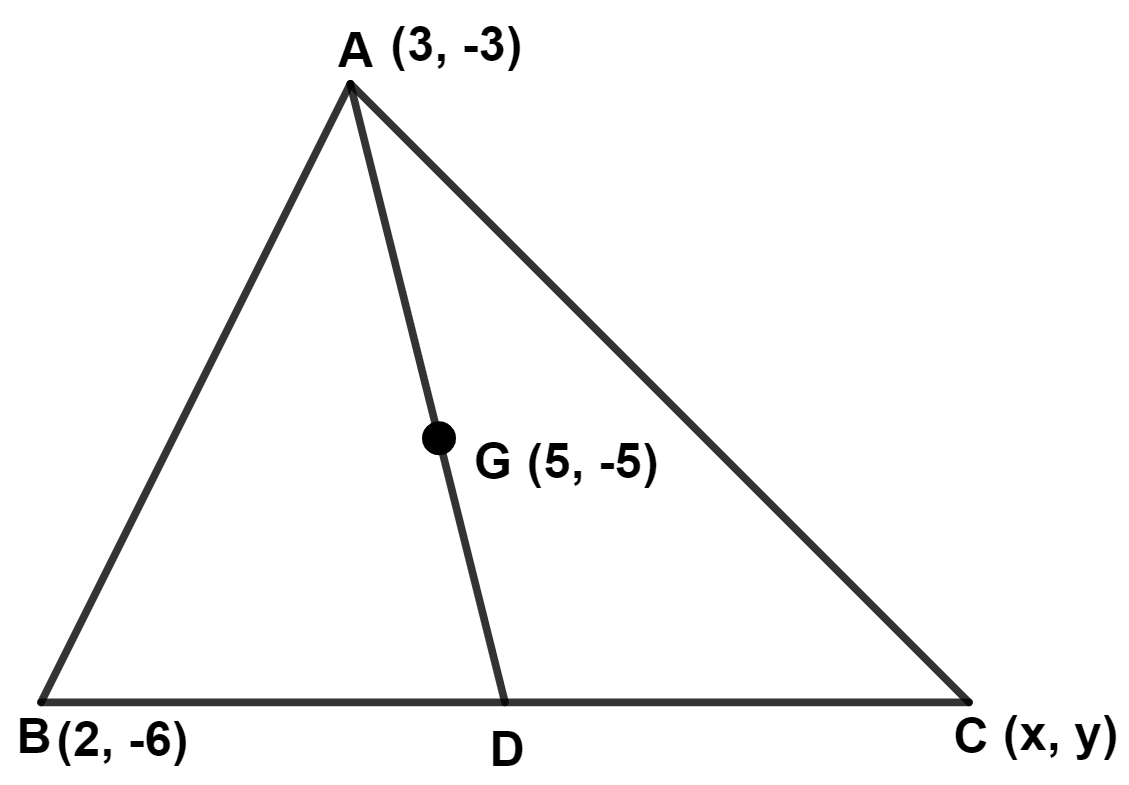
In the adjoining diagram, G is the centroid of △ ABC. A(3, -3), B(2, -6), C(x, y) and G(5, -5). The coordinates of point D are :
(2, -6)
(3, -6)
(6, -6)
(10, -6)
Answer
By formula,
Centroid of triangle =
C(x, y) = (10, -6).
Since, centroid is the point of intersection of all the three medians of a triangle.
∴ AD is the median.
∴ D is mid-point of BC.
Hence, Option 3 is the correct option.
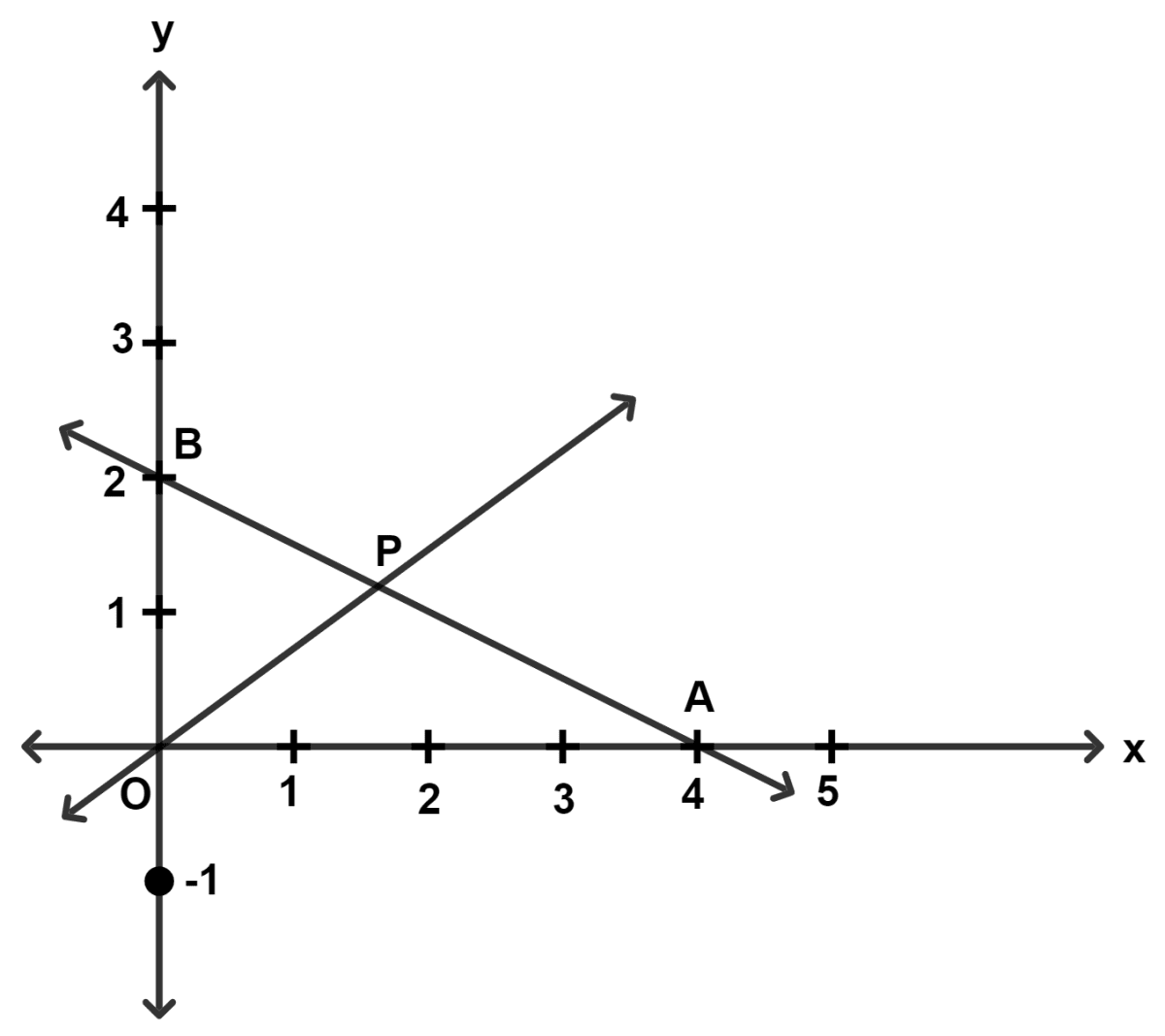
In the given diagram, O is the origin and P is the mid-point of AB. The equation of OP is :
y = x
2y = x
y = 2x
y = -x
Answer
From graph,
A = (4, 0) and B = (0, 2).
Given,
P is the mid-point of AB.
P = = (2, 1).
By two-point form,
⇒ y - y1 =
⇒ y - 1 =
⇒ y - 1 =
⇒ 2(y - 1) = x - 2
⇒ 2y - 2 = x - 2
⇒ 2y = x - 2 + 2
⇒ 2y = x.
Hence, Option 2 is the correct option.
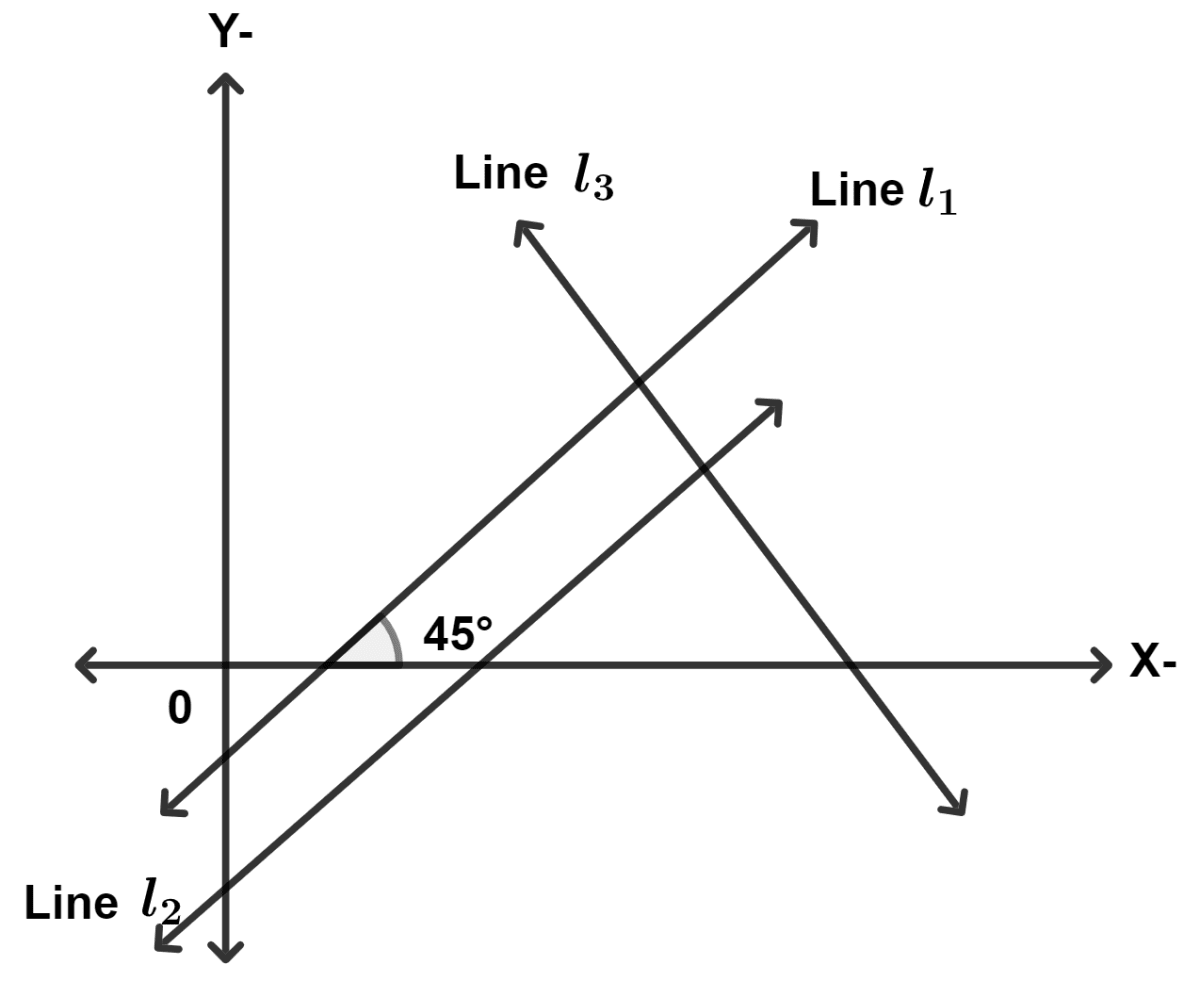
In the given figure line l1 is a parallel to line l2. If line l3 is perpendicular to line l1, then the slopes of lines l2 and l3 respectively are :
1, 1
-1, -1
1, -1
-1, 1
Answer
Slope of line l1 = tan 45° = 1.
We know that,
Slope of parallel lines are equal.
Slope of line l2 = Slope of line l1 = 1.
We know that,
Product of slope of perpendicular lines is equal to -1.
⇒ Slope of line l2 × Slope of line l3 = -1
⇒ 1 × Slope of line l3 = -1
⇒ Slope of line l3 = -1.
Hence, Option 3 is the correct option.
Which of the following lines cut the positive x-axis and positive y-axis at equal distances form the origin?
3x + 3y = 6
5x + 10y = 10
-x + y = 1
10x + 5y = 5
Answer
Substituting x = 0 in first equation,
⇒ 3(0) + 3y = 6
⇒ 3y = 6
⇒ y =
⇒ y = 2.
The line touches y-axis at point (0, 2).
Substituting y = 0 in first equation,
⇒ 3x + 3(0) = 6
⇒ 3x = 6
⇒ x =
⇒ x = 2.
The line touches y-axis at point (2, 0).
∴ Line 3x + 3y = 6 cuts positive x-axis and positive y-axis at equal distance i.e. 2 units form the origin.
Hence, Option 1 is the correct option.
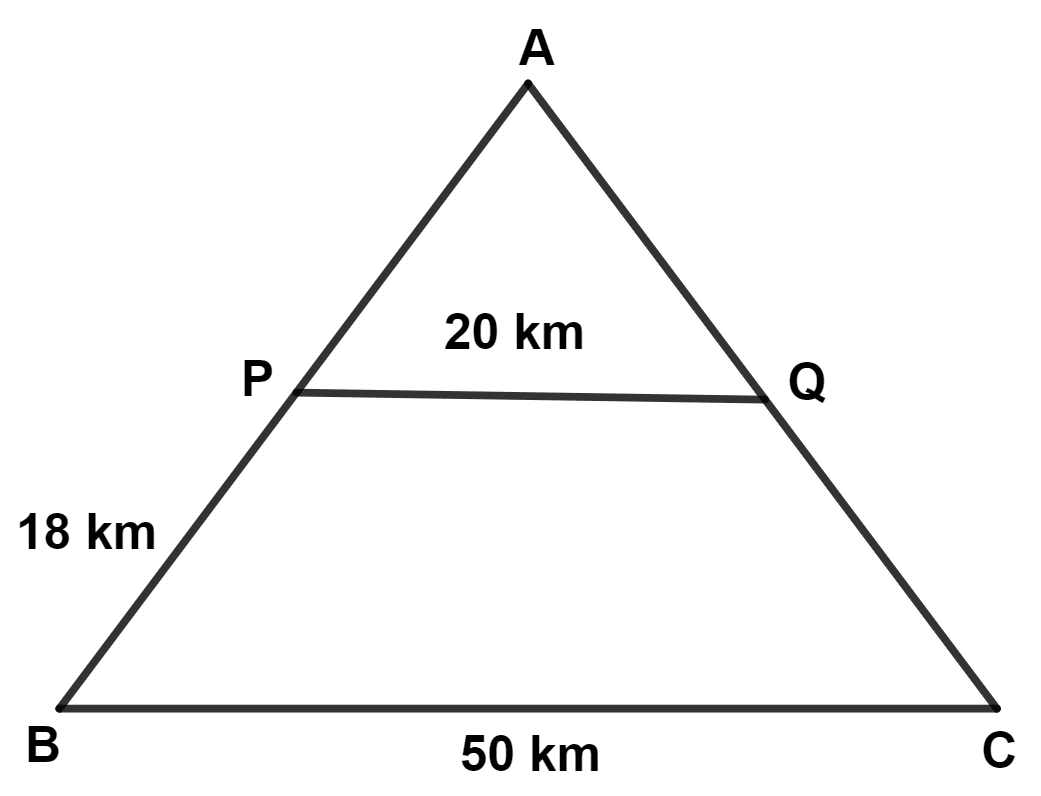
In the given diagram (not draw to scale), railway stations A, B, C, P and Q are connected by straight tracks. Track PQ is parallel to BC. The time taken by a train travelling at 90 km/hr to reach B from A by the shortest route is :
8 minutes
12 minutes
16.8 minutes
20 minutes
Answer
In △ APQ and △ ABC,
⇒ ∠PAQ = ∠BAC (Common angle)
⇒ ∠APQ = ∠ABC (Corresponding angles are equal)
∴ △ APQ ~ △ ABC (By A.A. axiom)
From figure,
Let AP = x km.
We know that,
Corresponding sides of similar triangle are proportional.
AB = AP + BP = 12 + 18 = 30 km.
Time = = 20 minutes.
Hence, Option 4 is the correct option.
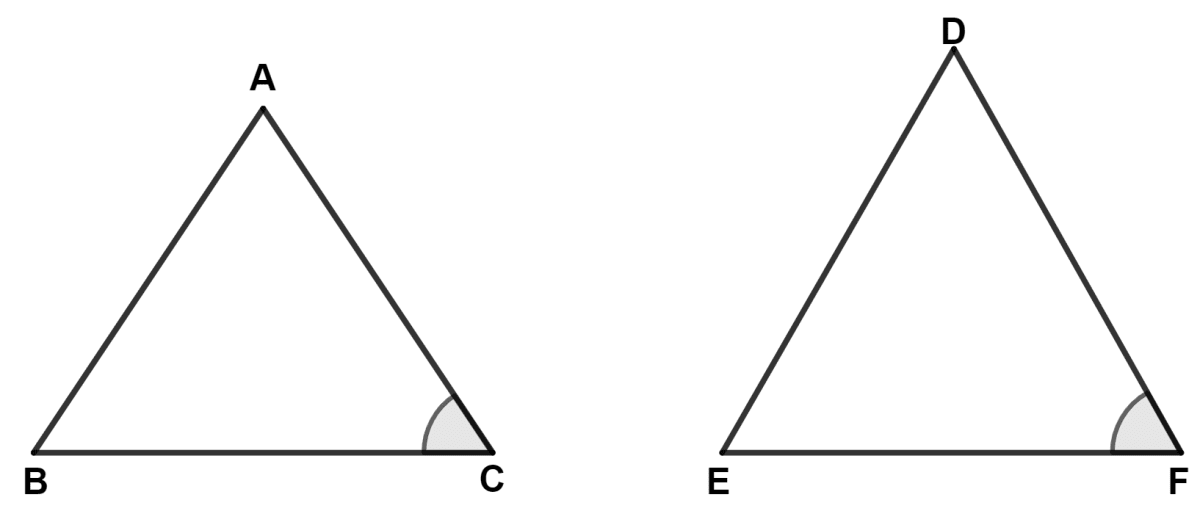
In the given diagram, △ ABC and △ DEF (not drawn to scale) are such that ∠C = ∠F and , then
△ ABC ~ △ DEF
△ BCA ~ △ DEF
△ CAB ~ △ DEF
the similarity of given triangles cannot be determined.
Answer
Given,
⇒ ∠C = ∠F
Since, the sides containing the angle may or may not be proportional,
i.e., we don't know if and are equal or not equal.
∴ Similarity of given triangles cannot be determined.
Hence, Option 4 is the correct option.
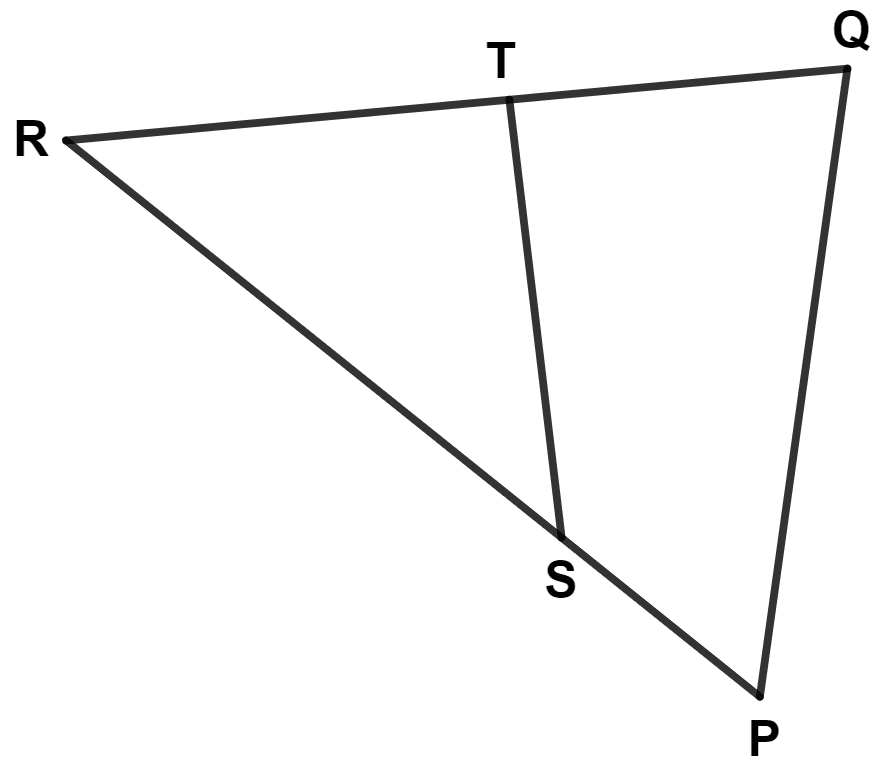
In the adjoining diagram, ST is not parallel to PQ. The necessary and sufficient conditions for △ PQR ~ △ TSR is :
∠PQR = ∠STR
∠QPR = ∠TSR
∠PQR = ∠TSR
∠PRQ = ∠RST
Answer
Given,
△ PQR ~ △ TSR.
From figure,
⇒ ∠PRQ = ∠SRT (Common angle)
The order of vertices of two similar triangles are written in such a way that the corresponding vertices occupy the same position.
∴ ∠PQR = ∠TSR
∴ △ PQR ~ △ TSR (By A.A. axiom)
Hence, Option 3 is the correct option.
The scale factor of a picture and the actual height of Sonia is 20 cm : 1.6 m. If her height in the picture is 18 cm, then her actual height is :
14.4 m
2.25 m
1.78 m
1.44 m
Answer
Scale factor of a picture and the actual height = 20 cm : 1.6 m = 20 cm : 160 cm
Hence, Option 4 is the correct option.
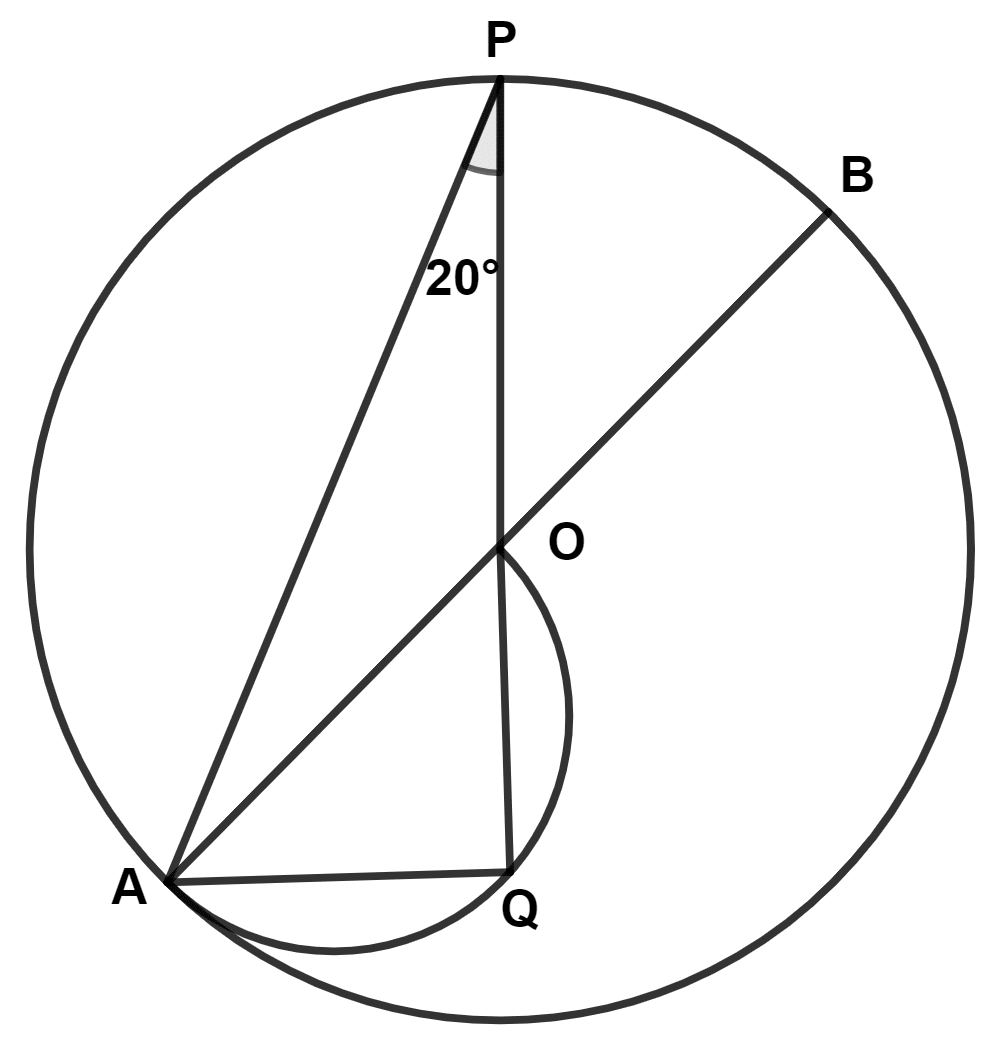
In the adjoining figure, O is the center of the circle, and a semicircle is drawn on OA as the diameter. ∠APQ = 20°. The degree measure of ∠OAQ is :
25°
40°
50°
65°
Answer
We know that,
Angle in a semi-circle is a right angle.
∴ ∠OQA = 90°
In △QAP,
⇒ ∠PQA + ∠QAP + ∠APQ = 180°
⇒ 90° + ∠QAP + 20° = 180°
⇒ ∠QAP = 180° - 90° - 20° = 70°.
In △OPA,
⇒ OA = OP (Radii of same circle)
⇒ ∠OAP = ∠OPA (Angle opposite to equal sides are equal)
⇒ ∠OAP = 20°.
From figure,
⇒ ∠OAQ = ∠QAP - ∠OAP = 70° - 20° = 50°.
Hence, Option 3 is the correct option.
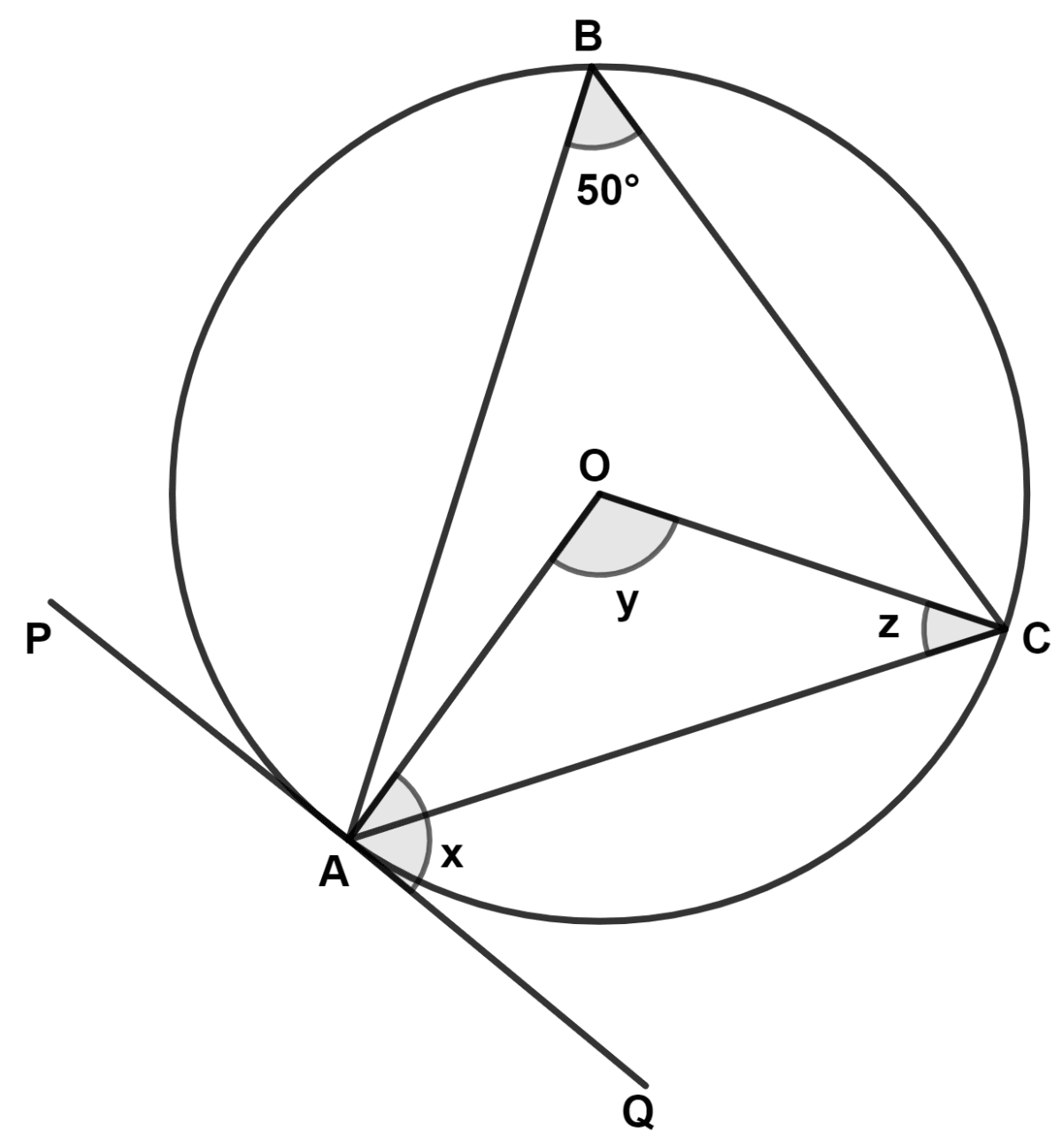
In the given diagram, O is the center of the circle, and PQ is a tangent at A. If ∠ABC = 50°, then values of x, y and z respectively are :
50°, 100°, 40°
50°, 50°, 65°
40°, 80°, 50°
50°, 25°, 78°
Answer
We know that,
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∴ ∠AOC (y) = 2∠ABC = 2 × 50° = 100°.
In △ AOC,
⇒ OA = OC (Radii of same circle)
⇒ ∠OAC = ∠OCA = z (Angle opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠OAC + ∠OCA + ∠AOC = 180°
⇒ z + z + 100° = 180°
⇒ 2z = 180° - 100°
⇒ 2z = 80°
⇒ z = = 40°.
We know that,
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
⇒ ∠CAQ (x) = ∠OAQ - ∠OAC = 90° - 40° = 50°.
Hence, Option 1 is the correct option.
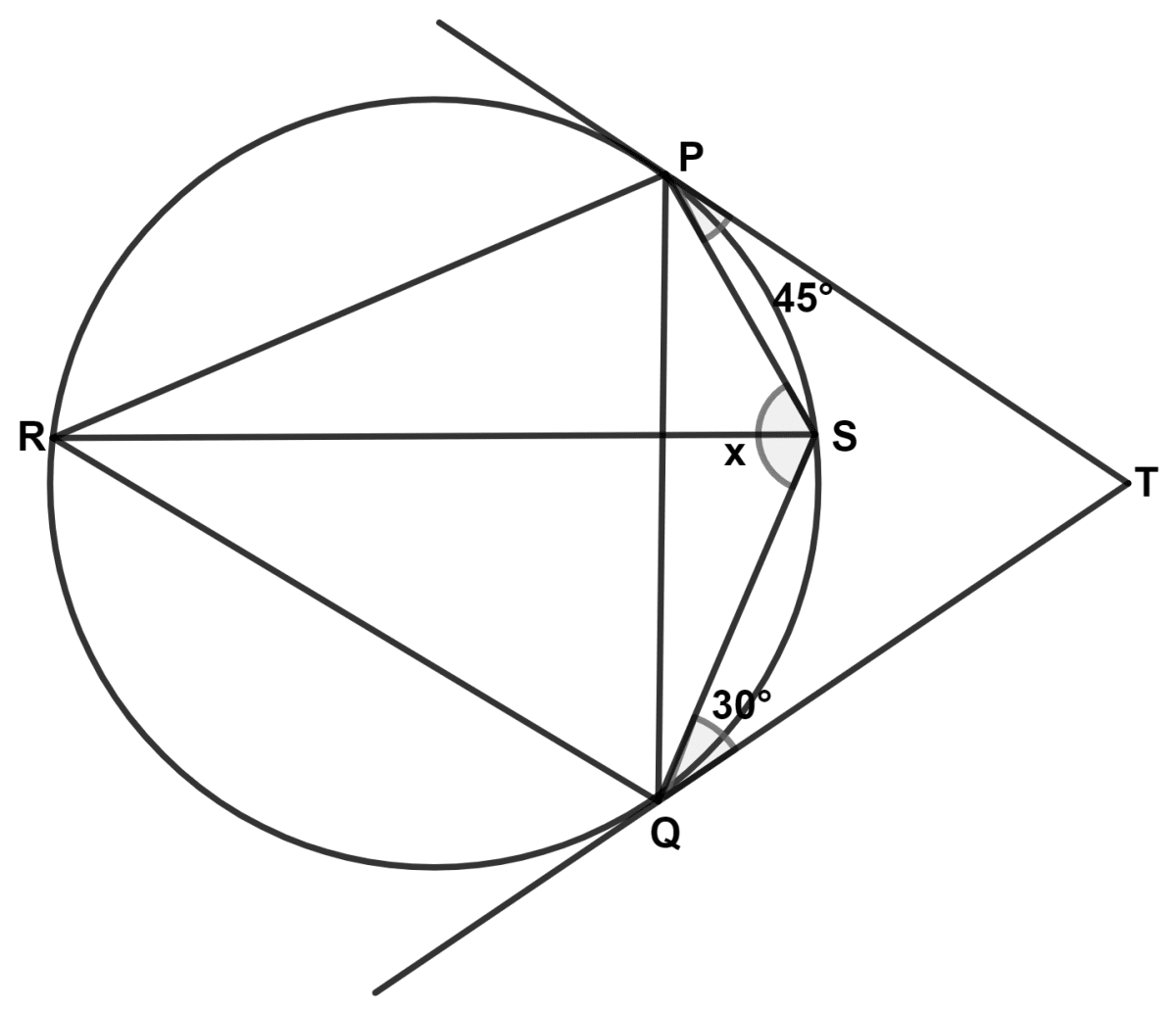
In the given figure, PT and QT are tangents to a circle such that ∠TPS = 45° and ∠TQS = 30°. Then, the value of x is :
30°
45°
75°
105°
Answer
We know that,
The angle between a tangent and a chord through point of contact is equal to an angle in the alternate segment.
∴ ∠SQP = ∠SPT = 45° and ∠SPQ = ∠SQT = 30°.
In △ SQP,
⇒ ∠SQP + ∠SPQ + ∠QSP = 180°
⇒ 45° + 30° + ∠QSP = 180°
⇒ 75° + ∠QSP = 180°
⇒ ∠QSP (x) = 180° - 75° = 105°.
Hence, Option 4 is the correct option.
A cylindrical metallic wire is stretched to double its length. Which of the following will NOT change for the wire after stretching?
Its curved surface area
Its total surface area
Its volume
Its radius
Answer
On changing the shape of a container, its volume remains same.
Hence, Option 3 is the correct option.
A right circular cone has the radius of the base equal to the height of the cone. If the volume of the cone is 9702 cu. cm, then the diameter of the base of the cone is :
21 cm
42 cm
cm
cm
Answer
Given,
Height of cone (h) = Radius of cone (r) = a cm (let)
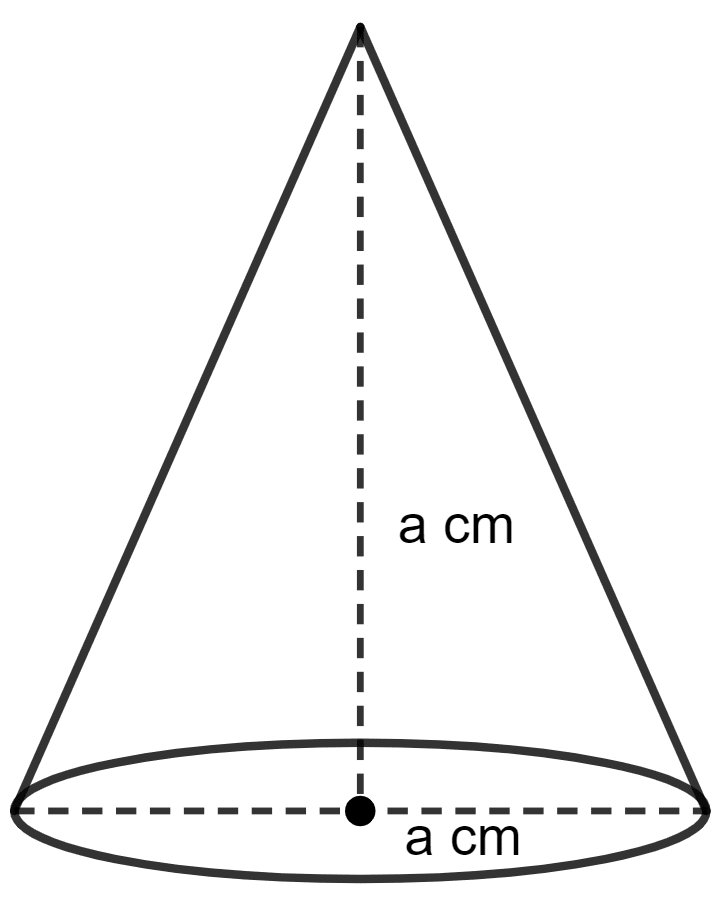
Given,
Volume = 9702 cm3
Diameter = 2 × radius = 2 × 21 = 42 cm.
Hence, Option 2 is the correct option.
A solid sphere with a radius of 4 cm is cut into 4 identical pieces by two mutually perpendicular planes passing through its center. Find the total surface area of one-quarter piece.
24π
32π
48π
64π
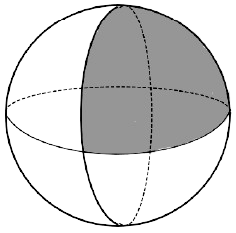
Answer
Total surface area of semi-hemisphere = 2πr2
= 2π × 42
= 2π × 16
= 32π.
Hence, Option 2 is the correct option.
Two identical solid hemispheres are kept in contact to form a sphere. The ratio of the total surface areas of two hemispheres to the surface area of the sphere formed is :
1 : 1
3 : 2
2 : 3
2 : 1
Answer
Let radius of hemisphere be r.
Total surface area of hemisphere = 3πr2
Total surface area of two hemisphere = 2 × 3πr2 = 6πr2.
Total surface area of sphere = 4πr2
Total surface area of two hemisphere : Total surface area of sphere = 6πr2 : 4πr2
= 6 : 4
= 3 : 2.
Hence, Option 2 is the correct option.
cosec2 θ + sec2 θ is equal to :
tan2 θ + cot2 θ
cot θ + tan θ
(cot θ + tan θ)2
1
Answer
Solving,
cosec2 θ + sec2 θ
= 1 + cot2 θ + 1 + tan2 θ
= cot2 θ + tan2 θ + 2
= (cot θ + tan θ)2
Hence, Option 3 is the correct option.
Given a = 3 sec2 θ and b = 3 tan2 θ - 2. The value of (a - b) is :
1
2
3
5
Answer
a - b = 3 sec2 θ - (3 tan2 θ - 2)
= 3 sec2 θ - 3 tan2 θ + 2
= 3(sec2 θ - tan2 θ) + 2
= 3(1) + 2
= 3 + 2
= 5.
Hence, Option 4 is the correct option.
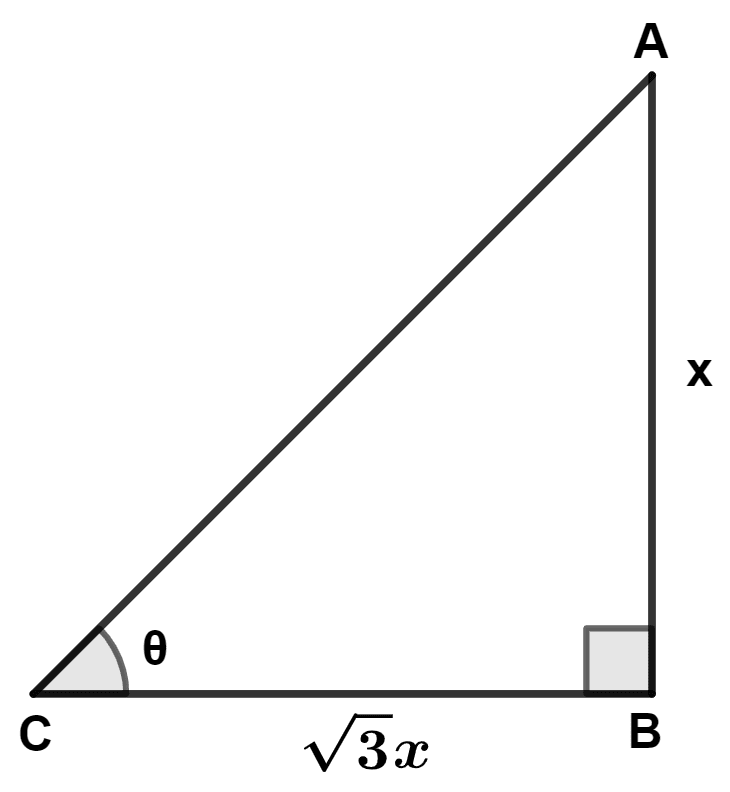
At a certain time of day, the ratio of the height of the pole to the length of its shadow is 1 : , then the angle of elevation of the sun at that time of the day is :
30°
45°
60°
90°
Answer
Let AB be the pole and BC be the shadow and angle of elevation of Sun be θ.
From figure,
⇒ tan θ =
⇒ tan θ =
⇒ tan θ =
⇒ tan θ = tan 30°
⇒ θ = 30°.
Hence, Option 1 is the correct option.
A man standing on a ship approaching the port towards the lighthouse is observing the top of the lighthouse. In 10 minutes, the angle of elevation of the top of the lighthouse changes from α to β. Then :
α > β
α < β
α = β
α ≤ β
Answer
Let A be the top of the lighthouse, C the initial position of ship and D be the position after 10 minutes.
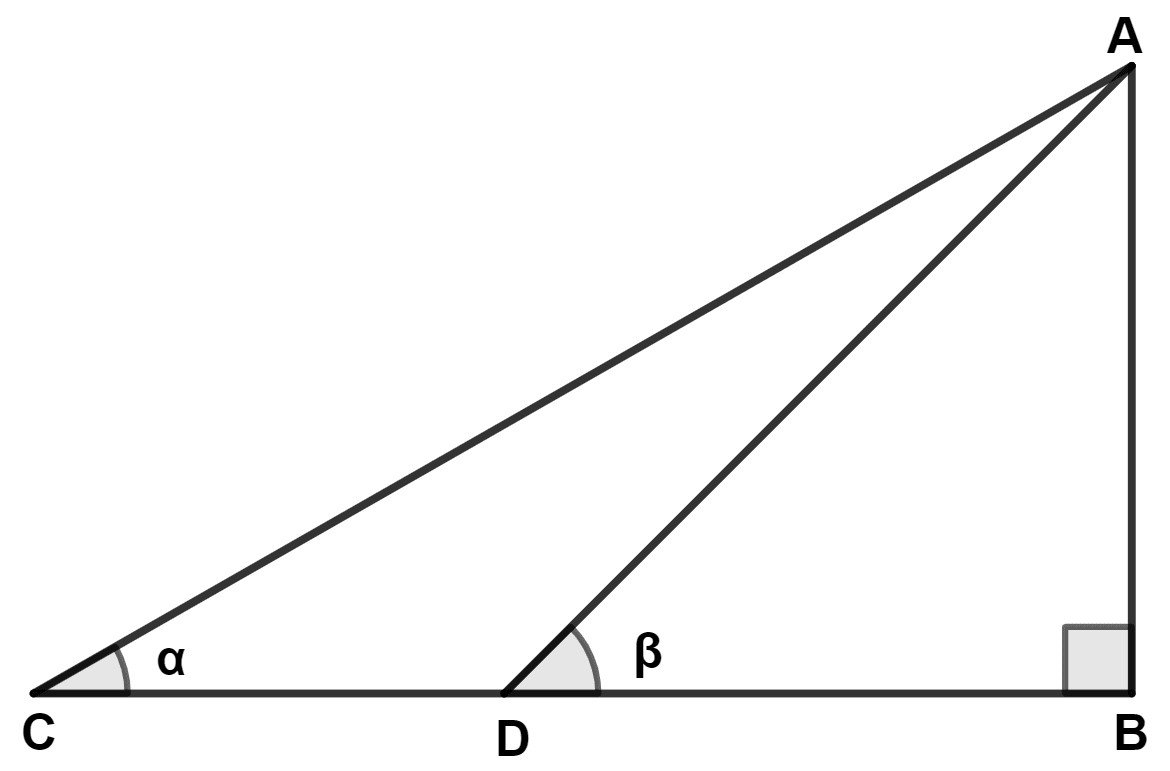
From figure,
tan α =
tan β =
Since, BC is greater than BD.
∴ tan α < tan β
⇒ α < β.
Hence, Option 2 is the correct option.
Assertion (A) : The difference in class marks of the modal class and the median class of the following frequency distribution table is 0.
| Class interval | Frequency |
|---|---|
| 20-30 | 1 |
| 30-40 | 3 |
| 40-50 | 2 |
| 50-60 | 6 |
| 60-70 | 4 |
Reason (R) : Modal class and median class are always the same for a given frequency distribution.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
Both A and R are true.
Answer
Cumulative frequency distribution table :
| Class interval | Class mark | Frequency | Cumulative frequency |
|---|---|---|---|
| 20-30 | 25 | 1 | 1 |
| 30-40 | 35 | 3 | 4 |
| 40-50 | 45 | 2 | 6 |
| 50-60 | 55 | 6 | 12 |
| 60-70 | 65 | 4 | 16 |
Median = = 8th term.
The 8th term lies in the class 50-60.
∴ Median class = 50-60
Also, frequency of class 50-60 is highest.
∴ Modal class = 50-60.
∴ Assertion (A) is true.
Modal class and median class are not always the same for a given frequency distribution.
∴ Reason (R) is false.
Hence, Option 3 is the correct option.
Assertion (A) : For a collection of 11 arrayed data, the median is the middle number.
Reason (R) : For the data 5, 9, 7, 13, 10, 11, 10, the median is 13.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
Both A and R are true.
Answer
For 11 arrayed data.
Median = th term
=
= 6th term, which will be the middle term.
∴ For a collection of 11 arrayed data, the median is the middle number.
∴ Assertion (A) is true.
Numbers = 5, 9, 7, 13, 10, 11, 10
Arranging in ascending order, we get :
5, 7, 9, 10, 10, 11, 13.
n = 7, which is odd.
Median = = 4th term = 10.
∴ Reason (R) is false.
Hence, Option 3 is the correct option.
Ankit has the option of investing in company A, where 7%, ₹ 100 shares are available at ₹ 120 or in company B, where 8%, ₹ 1000 shares are available at ₹ 1620.
Assertion (A) : Investment in Company A is better than Company B.
Reason (R) : The rate of income in Company A is better than in Company B.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is false, but R is true.
Both A and R are false.
Answer
In company A,
N.V. = ₹ 100
M.V. = ₹ 120
Dividend = 7% = = ₹ 7
∴ Investment = ₹ 120 and income = ₹ 7.
Income on ₹ 1 = = ₹ 0.0583
In company B,
N.V. = ₹ 1000
M.V. = ₹ 1620
Dividend = 8% = = ₹ 80
∴ Investment = ₹ 1620 and income = ₹ 80.
Income on ₹ 1 = = ₹ 0.0494
Since, rate of income is greater in company A.
∴ Assertion and Reason both are true and Reason is the correct explanation of Assertion.
Hence, Option 1 is the correct explanation.
Assertion (A) : x3 + 2x2 - x - 2 is a polynomial of degree 3.
Reason (R) : x + 2 is a factor of the polynomial.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
Both A and R are true.
Answer
x3 + 2x2 - x - 2 is a polynomial of degree 3.
By factor theorem,
(x - a) is a factor of f(x) if f(a) = 0.
x + 2 = 0
x = -2
Substituting x = -2 in x3 + 2x2 - x - 2, we get :
⇒ (-2)3 + 2(-2)2 - (-2) - 2
⇒ -8 + 2(4) + 2 - 2
⇒ -8 + 8 + 2 - 2
⇒ 0.
Hence, Option 4 is the correct option.
Assertion (A) : The point (-2, 8) is invariant under reflection in line x = -2
Reason (R) : If a point has its x-coordinate 0, it is invariant under reflection in both axes.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
Both A and R are true.
Answer
Point (-2, 8) lies on the line x = -2.
The point which lies on a line is invariant under reflection in the same line.
∴ (-2, 8) is invariant under reflection in line x = -2.
∴ Assertion (A) is true.
If a point has x-coordinate equal to 0 it means it lies on y-axis.
∴ It will be invariant under reflection in y-axis.
∴ Reason (R) is false.
Hence, Option 3 is the correct option.
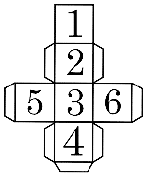
When a die is cast with numbering on its faces, as shown, the ratio of the probability of getting a composite number to the probability of getting a prime number is ............... .
2 : 3
3 : 2
1 : 3
1 : 2
Answer
From numbers 1 to 6
Prime numbers = 2, 3, 5.
Composite numbers = 4, 6.
Probability of getting a prime number = .
Probability of getting a composite number
= .
Probability of getting a composite number to probability of getting a prime number = = 2 : 3.
Hence, Option 1 is the correct option.
The product of A = and matrix M, AM = B where B = , then the order of matrix M is ............... .
2 × 2
2 × 1
1 × 2
4 × 1
Answer
Order of matrix A = 2 × 2
Order of matrix B = 2 × 1
Order of matrix M (let) = a × b
We know that,
Two matrix can be multiplied if the no. of columns of the first matrix is equal to the no. of rows of the second matrix and the resultant matrix has the no. of rows of first matrix and no. of columns of second matrix.
Given,
⇒ AM = B
⇒ A2 × 2 × Ma × b = B2 × 1
⇒ a = 2 and b = 1.
Order of matrix M = 2 × 1.
Hence, Option 2 is the correct option.
Given, a1, a2, a3, ..... and b1, b2, b3, ..... are real numbers such that a1 - b1 = a2 - b2 = a3 - b3 = ......... are all equal.
a1 - b1, a2 - b2, a3 - b3, ........ forms a ......... progression.
Geometric (r = 1)
Arithmetic (d = 1)
Geometric (r < 1)
Arithmetic (d = 0)
Answer
Since,
a1 - b1 = a2 - b2 = a3 - b3.
∴ a1 - b1, a2 - b2, a3 - b3, ........ forms a arithmetic progression with common difference (d = 0).
Hence, Option 4 is the correct option.
Locus of a moving point is ............... if it moves such that it keeps a fixed distance from a fixed point.
Circle
Line
Angle
Line segment
Answer
Locus of a moving point is circle if it moves such that it keeps a fixed distance from a fixed point.
Hence, Option 1 is the correct option.
The point of concurrence of the angle bisectors of a triangle is called the ............... of the triangle.
centroid
incenter
circumcenter
orthocenter
Answer
The point of concurrence of the angle bisectors of a triangle is called the incenter of the triangle.
Hence, Option 2 is the correct option.